Sabemos que a área de uma circunferência é diretamente proporcional ao tamanho do seu raio e é obtida fazendo π?r2, onde π equivale, aproximadamente, 3,14. O setor circular é uma parte da circunferência limitada por dois raios e um arco central. A determinação da área do setor circular depende da medida desse ângulo central e do comprimento do raio da circunferência.
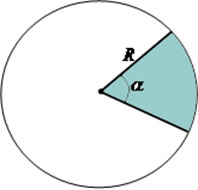
Como uma volta completa na circunferência equivale a 360o, podemos pensar da seguinte maneira para obter uma fórmula para calcular a área do setor circular:
360o -------------- π?r2
α ------------------ Asetor
Assim, teremos:
![]()
Onde,
α → é o ângulo central do setor circular.
r → é o raio da circunferência.
Vejamos alguns exemplos.
Exemplo 1. Determine a área do setor circular abaixo. (Use π = 3,14)
Solução: Como conhecemos o raio e a medida do ângulo central, basta substituir esses valores na fórmula da área do setor circular.
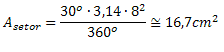
Exemplo 2. Numa circunferência de área igual a 121π cm2, calcule a área do setor circular delimitado por um ângulo central de 120o.
Solução: Para solução desse problema devemos verificar que no numerador da fórmula da área do setor circular, a medida do ângulo central α está multiplicando a área da circunferência, dessa forma teremos:
![]()
Videoaula relacionada:











