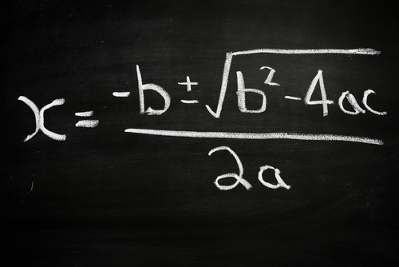A fórmula de Bhaskara é uma das alternativas de resolução de uma equação do 2° grau. Mas o que poucos sabem é que essa fórmula não foi desenvolvida pelo matemático Bhaskara! Na verdade, Bhaskara encontrou a fórmula para resolver equações do 2° grau em documentos feitos pelo matemático Shidhara provavelmente no século XI. Acredita-se que a fórmula leva o nome de Bhaskara por ter sido ele o primeiro a afirmar que uma equação do 2° grau pode ter dois resultados. Outro matemático famoso por estudar resoluções de equações do 2° grau foi al-Khowarizmi.
Mas o que são equações do 2° grau?
Trata-se de igualdades algébricas caracterizadas pela ocorrência de uma variável com expoente 2. Em geral, podemos dizer que uma equação do 2° grau é da forma ax² + bx + c = 0
A letra x é a incógnita, e as letras a, b e c são números reais que exercem a função de coeficientes. Para que a equação seja do 2° grau, é necessário que a ≠ 0. Além disso, se os coeficientes b e c forem nulos (iguais a zero), a equação será incompleta. As equações do 2° grau podem possuir até dois resultados, que são chamados de raízes da equação.
Agora que já sabemos o que é uma equação do 2° grau, vamos utilizar o método de al-Khowarizmi para deduzir a fórmula intitulada como “Fórmula de Bhaskara”. A ideia de al-Khowarizmi é modificar a equação do 2° grau até que ela se torne uma equação de 1° grau. Tome uma equação do 2° grau padrão:
ax² + bx + c = 0
Vamos mudar o coeficiente c para o segundo membro da igualdade:
ax² + bx = – c
Multiplicando ambos os lados da equação por 4a, teremos:
4a.(ax² + bx) = 4a.(– c)
4a²x² + 4abx = – 4ac
Vamos agora adicionar b² aos dois lados da igualdade:
4a²x² + 4abx + b² = – 4ac + b²
Observe que o primeiro membro da equação é um trinômio quadrado perfeito e podemos reescrevê-lo da seguinte forma:
(2ax + b)² = b² – 4ac
Considerando que o termo b² – 4ac é positivo, podemos extrair a raiz quadrada nos dois lados da equação:
![]()
Como a raiz quadrada de um termo ao quadrado é o próprio termo, podemos concluir que:
2ax + b = ![]()
Mas uma raiz quadrada pode ter dois resultados, um positivo e outro negativo. Sendo assim, a equação ficará como:
2ax + b = ± ![]()
Queremos encontrar o valor de x, portanto, precisamos isolá-lo no primeiro membro da igualdade. Dessa forma, b e 2a precisam passar para o segundo membro da igualdade:
2ax + b = ± ![]()
2ax = – b ± ![]()
![]()
Usualmente, utilizamos a letra grega Δ (delta) para representar o discriminante da equação b² – 4ac. Mas por que esse nome, discriminante?
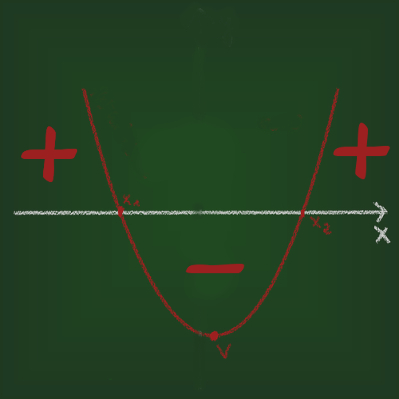
Porque o valor de Δ define quantas raízes a equação terá. Observe como o valor de Δ pode influenciar o resultado da equação do 2° grau:
Δ > 0 → a equação terá duas raízes;
Δ = 0 → a equação terá uma raiz;
Δ < 0 → a equação não terá raízes reais.
A partir da fórmula de Bhaskara, foram desenvolvidas as Relações de Girard, muito aplicadas na resolução de equações de 2° Grau.
Veja alguns exemplos de resolução de equações do 2° grau através da fórmula de Bhaskara:
Exemplo 1: x² + 3x – 4 = 0
Os coeficientes da equação são: a = 1, b = 3 e c = – 4. Vamos utilizar esses valores para calcular o valor de Δ:
Δ = b² – 4.a.c
Δ = 3² – 4.1.(– 4)
Δ = 9 + 16
Δ = 25
Como Δ > 0, podemos afirmar que a equação terá duas raízes. Vamos agora utilizar a fórmula de Bhaskara, substituindo o discriminante b² – 4ac por Δ:
![]()
x = – 3 ± √25
2.1
x = – 3 ± 5
2
Podemos ter dois resultados:
x1 = – 3 + 5 = 2 = 1
2 2
x2 = – 3 – 5 = – 8 = – 4
2 2
Portanto, a equação x² + 3x – 4 = 0 possui as raízes x1 = 1 e x2 = – 4.
Exemplo 2: 2x² – 4x = 0
Os coeficientes da equação são: a = 2 e b = – 4. Como c = 0, essa equação é incompleta. Calculemos o valor de Δ:
Δ = b² – 4.a.c
Δ = (– 4)² – 4.2.0
Δ = 16 – 0
Δ = 16
Como Δ > 0, a equação terá duas raízes. Através da fórmula de Bhaskara, temos:
![]()
x = – (– 4) ± √16
2.2
x = 4 ± 4
4
x1 = 4 + 4 = 8 = 2
4 4
x2 = 4 – 4 = 0 = 0
4 4
Portanto, x1 = 2 e x2 = 0 são soluções da equação 2x² – 4x = 0.
Exemplo 3: x² – 2x + 16 = 0
Os coeficientes da equação são: a = 1 e b = – 2 e c = 16. Vamos calcular o valor de Δ:
Δ = b² – 4.a.c
Δ = (– 2)² – 4.1.16
Δ = 4 – 64
Δ = – 60
Como Δ < 0, a equação não possui raízes reais.
Aproveite para conferir nossas videoaula relacionadas ao assunto: