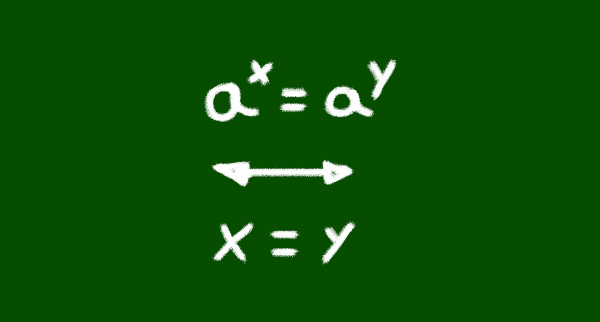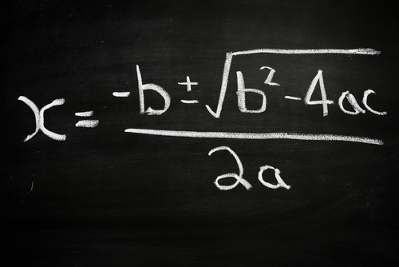Equação exponencial é uma equação que possui incógnitas no expoente. Para encontrar as possíveis soluções dessa equação, buscamos igualar as bases nos dois membros da igualdade para que seja possível igualar os expoentes. Para resolvê-la, é fundamental que se conheçam as propriedades da potenciação, pois, a partir dessas propriedades, conseguimos igualar as bases dos dois lados da igualdade e posteriormente igualar os expoentes.
Esse tipo de equação é bastante recorrente em fenômenos que se comportam de forma exponencial, como reprodução de bactérias, índice de contaminação de um vírus, juros compostos, entre outras várias situações presentes no nosso dia a dia.
Leia também: Função exponencial — aquela que sua variável está no expoente
Tópicos deste artigo
- 1 - Resumo sobre equação exponencial
- 2 - Videoaula sobre equação exponencial
- 3 - O que é equação exponencial?
- 4 - Quais são as propriedades de potência?
- 5 - Potência com expoente fracionário
- 6 - Passo a passo para resolver uma equação exponencial
- 7 - Exercícios resolvidos sobre equação exponencial
Resumo sobre equação exponencial
-
Conhecemos como equação exponencial uma equação que possui a incógnita em seu exponente.
-
As equações exponenciais são utilizadas para compreender fenômenos que se comportam de forma exponencial, como a reprodução de bactérias, os juros compostos, entre outras situações.
-
Para resolver uma equação exponencial, buscamos igualar as bases dos dois membros da equação para poder igualar os expoentes.
-
O entendimento das propriedades da potenciação é essencial para aplicar na resolução de equações exponenciais.
Videoaula sobre equação exponencial
O que é equação exponencial?
No nosso dia a dia, existem várias grandezas que se comportam de forma exponencial, como o juro composto, que é bastante comum nas relações financeiras, mas também há outros exemplos, como medição da radiação de um elemento químico, índice de contaminação de um vírus, reprodução bacteriana, etc. Diante da necessidade de compreensão desses fenômenos, surgiram as equações exponenciais.
Conhecemos como equação exponencial qualquer equação que possua uma incógnita no expoente. Veja a seguir alguns exemplos de equações exponenciais a seguir.
-
3x = 9
-
4x+2 = 1024
-
8x – 5 = 512
-
2x² – 4 = 8– x
Quais são as propriedades de potência?
Para encontrar as soluções de uma equação exponencial, é fundamental dominar as propriedades de potência:
-
igualdade de potência de mesma base;
-
multiplicação de potência de mesma base;
-
divisão de potência de mesma base;
-
potência de potência;
-
potência com expoente negativo;
-
potência com expoente fracionário.
-
Igualdade de potência de mesma base
Essa é a principal propriedade que utilizamos para resolver as equações exponenciais. Se existe a igualdade entre duas potências de mesma base, então consequentemente o expoente é igual.
a n = a m → n = m
-
Multiplicação de potências de mesma base
Ao realizar a multiplicação entre duas potências de mesma base, podemos representar essa multiplicação como uma única potência, conservando a base e somando os expoentes.
a n · a m = a n+m
-
Divisão de potências de mesma base
Ao realizar a divisão entre duas potências de mesma base, podemos representar essa divisão como uma única potência, conservando a base e subtraindo os expoentes.
a n : a m = a n – m
-
Potência de potência
Quando calculamos a potência de uma potência, podemos reescrever essa potência conservando a base e multiplicando os seus expoentes.
(a n) m = a n · m
-
Potência com expoente negativo
Quando o expoente da potência é negativo, podemos torná-lo positivo escrevendo o inverso da base.
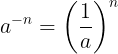
Potência com expoente fracionário
Ao resolver problemas com expoente fracionário, é possível transformá-lo em uma raiz. É importante saber que o contrário também vale, ou seja, é possível reescrever uma raiz como uma potência de expoente fracionário.
![]()
Leia também: Equação polinomial — uma expressão envolvendo um polinômio e uma igualdade
Passo a passo para resolver uma equação exponencial
Para encontrar as soluções de uma equação exponencial, utilizamos as propriedades supracitadas como meio de simplificar ao máximo os dois membros da igualdade, com o objetivo final de poder igualar as bases e os expoentes da equação.
Ao igualar os expoentes, temos uma nova equação, mas polinomial. Equações polinomiais, quando são do 1º grau, podem ser resolvidas isolando a incógnita; quando são do 2º grau, podemos utilizar alguma das técnicas conhecidas para resolver equações desse tipo, como soma e produto ou a fórmula de Bhaskara. Vejamos alguns exemplos.
Exemplo 1:
3x = 81
Na busca por igualar as bases, podemos reescrever 81 como uma potência de base 3. Sabemos que 81 = 34, logo:
3x = 81
3x = 34
Note que encontramos uma igualdade de potência de mesma base, então consequentemente podemos igualar os expoentes:
3x = 34
x = 4
Exemplo 2:
4x · 16 = 1024
Primeiro vamos fatorar cada um dos números reescrevendo-os como uma potência de base 2.
4 = 2²
16 = 24
1024 = 210
Então, temos que: (22)x · 24 = 210.
Note que temos uma potência de potência: (2²)x = 22x.
22x · 24 = 210
No primeiro membro, há uma multiplicação de potência de mesma base. Podemos conservar essa base e somar os expoentes:
22x+4 = 210
Veja que as bases estão iguais. Como há uma igualdade entre potências de mesma base, então podemos igualar os expoentes:
22x+4 = 210
2x + 4 = 10
Agora basta resolver a equação do 1º grau:
2x = 10 – 4
2x = 6
x = 6 : 2
x = 3
Exemplo 3:
2x² – 4 = 8– x
Fatorando o 8, sabemos que 8 = 2³.
2x² – 4 = 8– x
2x² – 4 = (2³)– x
Calculando a potência de potência, temos que:
2x² – 4 = (2³)– x
2x² – 4 = 2 –3x
Agora que as bases são iguais, podemos igualar os expoentes:
2x² – 4 = 2 –3x
x² – 4 = – 3x
Encontramos uma equação do 2º grau, logo é necessário resolvê-la:
x² – 4+ 3x = 0
x² + 3x – 4 = 0
-
a = 1
-
b = 3
-
c = – 4
Δ = b² – 4ac
Δ = 3² – 4 · 1 · (– 4)
Δ = 9 + 16
Δ = 25
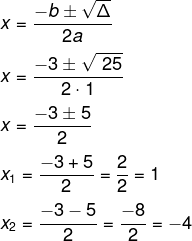
Então, o conjunto de soluções dessa equação exponencial é o conjunto S {– 4, 1}.
Exercícios resolvidos sobre equação exponencial
Questão 1 — (Contemax — Prefeitura de Coremas) Em uma certa empresa do Nordeste responsável por certo tipo de pesquisas, constatou-se que a população (P) de um determinado tipo de bactéria cresce segundo a expressão P(t) = 25 · 2t , onde t representa o tempo em horas. Para atingir uma população de 200 bactérias, será necessário um tempo de:
A) 1 hora.
B) 1 hora e 30 minutos.
C) 3 horas.
D) 4 horas e 30 minutos.
E) 5 horas.
Resolução
Alternativa C.
Temos que P(t) = 200. Substituindo na equação, temos que:
200 = 25 · 2t
200 : 25 = 2t
8 = 2t
Sabemos que 8 = 2³.
23 = 2t
t = 3 horas
Questão 2
Qual é o valor de x que faz com que a equação 2x+1 + 2x+2 = 96 seja verdadeira?
A) 1
B) 2
C) 3
D) 4
E) 0
Resolução:
Alternativa D.
Pela propriedade de potência, sabemos que:
2x+ 1 = 2x · 21
2x+ 2 = 2x ·2²
Substituindo na equação:
2x · 21 + 2x ·2² = 96
2x · 2 + 2x ·4 = 96
Colocando 2x em evidência, temos que:
2x (2 + 4) = 96
2x · 6 = 96
2x = 96 : 6
2x = 16
Agora para igualar as bases, sabemos que 16 = 24.
2x = 24
Como as bases são iguais, podemos igualar os expoentes, ou seja, x = 4.