Do ponto de vista analítico, circunferência é o conjunto dos pontos P(x, y) do plano que equidistam (apresentam a mesma distância) de um ponto O. Essa distância é chamada de raio r. É importante deixar claro que circunferência e círculo são formas geométricas distintas. Enquanto o círculo é formado por todos os pontos do contorno e do interior, a circunferência corresponde somente aos pontos que estão no contorno.
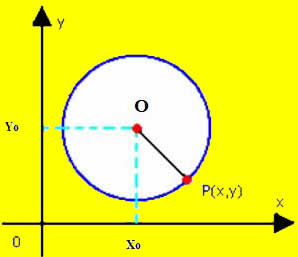
Vamos obter a equação reduzida da circunferência de centro O (x0, y0) e raio r. Como foi definido anteriormente, circunferência é o conjunto dos pontos P(x, y) do plano, tais que:
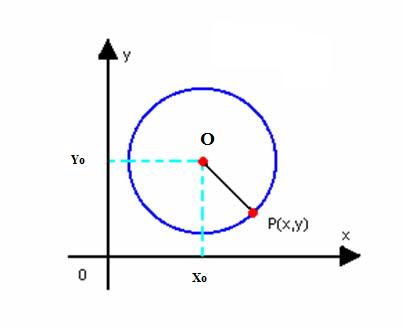
Temos que:
dP,O = r
ou
![]()
Elevando os dois membros ao quadrado, obtemos:
![]()
Que é a equação reduzida da circunferência de raio r e centro O (x0, y0).
Exemplo 1. Determine a equação reduzida da circunferência de centro O(5, 7) e raio 4.
Solução: Como sabemos as coordenadas do centro da circunferência e a medida do raio, temos que:
O(5, 7) → x0 = 5 e y0 = 7
r = 4
Substituindo esses valores na equação reduzida da circunferência, obtemos:
(x - 5)2 + (y - 7)2 = 42
Ou
(x - 5)2 + (y - 7)2 = 16 → Equação reduzida da circunferência de centro O(5, 7) e raio 4.
Exemplo 2. Determine as coordenadas do centro e a medida do raio da circunferência de equação:
(x - 3)2 + (x - 8)2 = 121
Solução: Sabemos que a equação reduzida da circunferência é do tipo:
(x - x0 )2 + (y - y0 )2 = r2
Assim, podemos concluir que:
x0 = 3 e y0 = 8 → O(3, 8)
r2 = 121 → r = 11
Exemplo 3. Encontre as coordenadas do centro e o valor do raio da circunferência de equação:
a) x2 + y2 = 25
Solução: A equação reduzida da circunferência é do tipo:
(x - x0 )2 + (y - y0 )2 = r2
Assim, temos que:
x0 = 0 e y0 = 0 → O(0, 0)
r2 = 25 → r = 5 cm
Observação: Toda circunferência com centro na origem tem equação reduzida da forma:
x2 + y2 = r2
b) (x + 2)2 + (y - 9)2 = 3
Solução: A equação reduzida da circunferência é da forma:
(x - x0 )2 + (y - y0 )2 = r2
Então,
x0 = – 2 e y0 = 9 → O(– 2, 9)
r2 = 3 → r = √3