A realização de cálculos sobre meia-vida é muito comum no estudo de amostras radioativas para determinar a porcentagem em massa de material radioativo ou a própria massa do material ainda existente.
É importante lembrar que a meia-vida de um material radioativo é o período necessário para que ele perca metade do seu poder radioativo ou de sua massa. Se um determinado material radioativo apresenta uma meia-vida de 30 anos, após esse período, é certo que ele apresentará apenas metade do poder radioativo possuía. Se o poder radioativo fosse de 100%, após 30 anos, ele teria apenas 50% desse poder.
Se um texto ou um exercício não fornecer o período de meia-vida de um isótopo, mas um gráfico, a meia-vida poderá ser determinada pela análise desse gráfico. Para isso, basta utilizar a referência do 50% restantes de material:
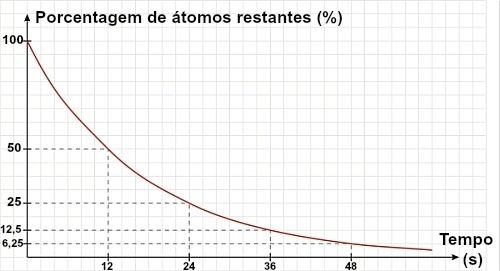
No gráfico acima, podemos observar que a meia-vida do material é de 12 s.
Meia-vida em porcentagem
Quando o cálculo da meia-vida envolve porcentagem, podemos utilizar a seguinte fórmula para obter a resolução:
Pr = Po
2x
-
Pr = porcentagem de material radioativo que resta na amostra;
-
Po = porcentagem inicial de material radioativo que havia na amostra (sempre será 100%);
-
x= número de meias-vidas que se passaram.
Exemplo: (UFPI) Um elemento radioativo tem um isótopo cuja meia-vida é 250 anos. Qual a porcentagem da amostra inicial desse isótopo que existirá após 1000 anos?
a) 1,25%
b) 4%
c) 6,25%
d) 12,5%
e) 25%
Nesse exemplo, os dados fornecidos foram:
-
Meia-vida = 250 anos
-
Tempo em que a amostra eliminou radiação = 1000 anos
-
Porcentagem inicial = 100% (padrão de amostras radioativas)
1o Passo: calcular o número de meias-vidas que se passaram após 1000 anos.
Para isso, basta dividir o tempo final pela meia-vida:
x = 1000
250
x = 4
2o Passo: calcular a porcentagem de material radioativo após 1000 anos na fórmula a seguir:
Pr = Po
2x
Pr = 100
24
Pr = 100
16
Pr = 6,25%
Meia-vida em fração
Quando o cálculo da meia-vida envolve fração, podemos utilizar a seguinte fórmula para obter a resolução:
F = No
2x
-
F = fração referente ao material radioativo que resta na amostra;
-
No = quantidade que existia na amostra radioativa (100% ou o número 1);
-
x = número de meias-vidas que se passaram.
Exemplo: Um determinado isótopo de iodo radioativo é utilizado para diagnóstico de doenças da glândula tireoide. Partindo-se de uma massa (inteira) do isótopo, após 24 dias, sobra 1/8. Qual é a meia-vida desse isótopo?
a) 24 dias
b) 8 dias
c) 12 dias
d) 16 dias
e) 4 dias
-
Meia-vida = ?
-
Tempo em que a amostra eliminou radiação = 24 dias
-
Massa inicial = 1 (padrão de amostras radioativas)
-
Massa final = 1/8
1o Passo - Calcular o número de meias-vidas que se passaram pela amostra na fórmula a seguir:
1 = 1
8 2x
2x = 8
2x = 23
x = 3
2o Passo - Calcular a meia-vida a partir do número de meias-vidas passadas e do tempo total:
Meia-vida = 24
3
Meia-vida = 8 dias
Meia-vida em massa
mr = mo
2x
-
mr = massa de material radioativo que resta na amostra;
-
mo = massa inicial de material radioativo que havia na amostra;
-
x = número de meias-vidas que se passaram.
Exemplo: (Unirio-RJ) O Tl2O1 é um isótopo radioativo usado na forma de TlCl3 (cloreto de tálio) para diagnóstico do funcionamento do coração. Sua meia-vida é de 73 h ( ≅ 3 dias). Certo hospital possui 20 g desse isótopo. Sua massa, em gramas, após 9 dias, será igual a:
a) 1,25
b) 3,3
c) 7,5
d) 2,5
e) 5,0
-
Meia-vida = 3 dias
-
Tempo em que a amostra eliminou radiação = 9 dias
-
Massa inicial = 20 g
1o Passo: calcular o número de meias-vidas que se passaram após 9 anos.
x = 9
3
x = 3
2o Passo: calcular a massa do material radioativo restante após 9 dias.
mr = mo
2x
mr = 20
23
mr = 20
8
mr = 2,5g






