Ao estudarmos os conceitos iniciais sobre colisões, vimos que durante as colisões os corpos envolvidos trocam forças muito grandes, que provocam deformação nos corpos. Essas forças recebem o nome de forças impulsivas e são forças internas em relação ao sistema, constituído pelos corpos envolvidos na colisão. Mesmo tendo forças externas atuando no sistema, elas são consideradas nulas. Dessa forma, caracterizamos uma colisão como um sistema isolado de forças externas, que apresenta, então, conservação da quantidade de movimento.
A fase que antecede uma colisão é denominada aproximação, e a fase que sucede uma colisão, é denominada afastamento. Uma forma básica para se classificar uma colisão é levar em consideração a velocidade relativa de afastamento, ou seja, tomar como base a velocidade logo após a colisão e a velocidade relativa de aproximação, ou seja, tomar como base a velocidade que antecede a colisão.
Partindo desses princípios, velocidades de aproximação e afastamento, podemos determinar as velocidades relativas do sistema na fase de aproximação e de afastamento. Sendo assim, as velocidades relativas podem ser definidas da seguinte maneira:
- na fase de aproximação: ![]() (uma vez que V1 > V2)
(uma vez que V1 > V2)
- na fase de afastamento: ![]() (visto que V’2 > V’1)
(visto que V’2 > V’1)
Em física chamamos de coeficiente de restituição (e) a relação entre os valores positivos, ou seja, valores em módulo, das velocidades relativas de afastamento e de aproximação:
A relação entre os módulos das velocidades relativas de afastamento e o módulo da velocidade relativa de aproximação chama-se coeficiente de restituição (e):
![]()
Caso particular:
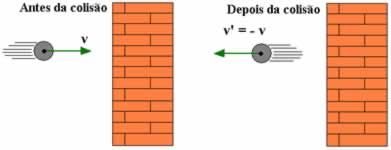
Uma situação bastante importante que devemos ressaltar é quando a massa de um dos corpos que colidem é muito maior do que a do outro. Como exemplo podemos citar uma bolinha se colidindo contra uma parede. Nesse caso, a fim de simplificar, equacionamos o choque pelo coeficiente de restituição, dessa forma levamos em consideração que a velocidade do corpo, cuja massa é muito maior, não sofre variação alguma. Para essa situação consideramos que a velocidade do corpo de massa maior é V = 0, de tal modo, temos:
![]()
Sendo assim, podemos dizer que o coeficiente de restituição depende apenas da velocidade do corpo de menor massa.


