Quando vemos vídeos de catástrofes envolvendo furacões, geralmente observamos os telhados das casas e construções indo pelos ares. Por essa razão, é comum pensarmos que a força e a velocidade do vento são tão grandes que arrancam tudo o que está pelo caminho. Todavia, a explicação para tal desastre está na equação de Bernoulli, que nos mostra o comportamento de um fluido em escoamento.
A chamada equação de Bernoulli foi proposta no século XVII por Daniel Bernoulli, que realizou estudos sobre o escoamento de fluidos. Essa equação não é um princípio novo, mas, sim, uma reformulação da conhecida Lei de Stevin, utilizada para fluidos em repouso. A equação de Bernoulli é dada por:
P + ½ ρv2 + ρgy = Constante
Na equação, P é a pressão exercida pelo fluido, v é a velocidade de escoamento, g é a gravidade, ρ é a densidade do fluido e y é a altura. Algo importante que essa equação evidencia é que, tomando duas regiões no espaço em que não há diferença de altura, a velocidade e a pressão exercida pelo fluido serão inversamente proporcionais.
Para duas regiões no espaço que não apresentam diferença de altura, temos:
P1 + ½ ρv12 = P2 + ½ ρv22
A partir dessa igualdade, podemos entender que, quanto maior for a velocidade de escoamento de um fluido, menor será a pressão exercida por ele e vice-versa. Portanto, no caso dos furacões, a alta velocidade do vento passando rente aos telhados diminui muito a pressão naquela região, tornando a pressão interna das casas maior que a externa, o que gera uma força ascendente capaz de empurrar e arrancar o telhado.
Ainda como aplicação dessa equação, podemos citar as asas das aeronaves, que são projetadas para que a velocidade do vento seja maior na parte superior, diminuindo a pressão do ar e gerando uma força ascendente denominada de força de sustentação.
Outra equação importante quando nos referimos a fluidos em escoamento é a equação da continuidade, que nos mostra a relação inversa entre a área de escoamento e a velocidade do fluido.
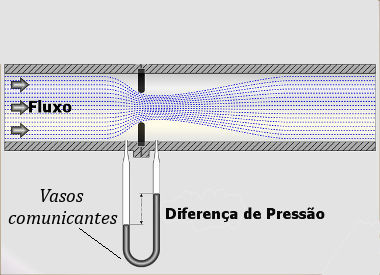
A imagem acima mostra que, quando houve diminuição da área de escoamento, ocasionando aumento de velocidade, ocorreu, segundo a proposta de Bernoulli, diminuição de pressão, indicada pela maior altura do fluido na parte direita dos vasos comunicantes.