Equilíbrio de um ponto material
Consideramos como ponto material um corpo cuja dimensão tenha tamanho desprezível em relação a um determinado referencial. O equilíbrio de um ponto material tem suas condições definidas pela Primeira Lei de Newton, que diz o seguinte:
“Um ponto material está em equilíbrio se a resultante das forças que atuam sobre ele é nula”.
Veja o exemplo na figura a seguir:
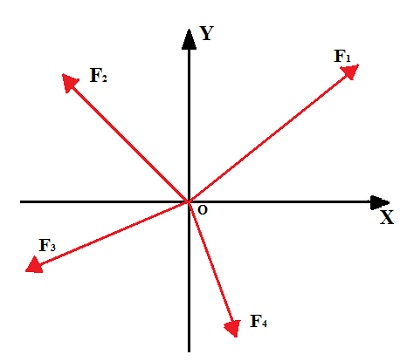
Sobre o ponto O estão aplicadas quatro forças F1, F2, F3 e F4
Conforme mostra a figura, sobre o ponto O estão sendo exercidas as forças F1, F2, F3 e F4 . Para que haja equilíbrio, é necessário que a resultante desse sistema de forças seja igual a zero. As forças representadas acima são vetores, sendo assim, para que a resultante dessas forças seja nula, a soma das componentes nas direções x e y devem ser nulas. Dessa forma, temos que para o eixo x:
F1X + F2X + F3X + F4X = 0
E para o eixo y:
F1Y+ F2Y + F3Y + F4Y = 0
A partir dessas equações, podemos generalizar os resultados e descrever essa equação utilizando as fórmulas:
ΣFX = 0 e ΣFy = 0
Sendo que:
ΣFX é a soma algébrica dos componentes das forças do eixo x;
ΣFy é a soma algébrica dos componentes das forças do eixo y.
Equilíbrio de corpos rígidos
Para estudar o equilíbrio de corpos rígidos, devemos considerar que esses materiais podem deslocar-se ou girar. Portanto, devemos considerar duas condições para o equilíbrio:
-
A resultante das forças exercidas sobre o corpo deve ser nula;
-
A soma dos momentos das forças que atuam sobre ele também deve ser nula.
Para compreender melhor a segunda condição, vejamos a figura a seguir:
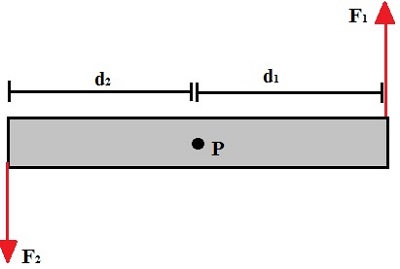
Sistema de forças atuando sobre um corpo e provocando movimento de rotação
O efeito das forças 1 e 2 sobre a barra da figura está relacionado com a rotação que ela sofrerá. O momento de força MF é definido como o produto da força pela distância ao ponto P. Sendo assim, para a força F1:
MF1 = F1 . D1
E para a força F2:
MF2 = - F2 . D2
Em razão de o sentido da força F2 favorecer o movimento de rotação anti-horário, o sinal é negativo.
De acordo com a segunda condição de equilíbrio, a soma dos momentos de força deve ser nula. Aplicando essa condição à barra do exemplo acima, teremos:
MF1 + MF2 = 0
F1 . D1 - F2 . D2 = 0
Essa condição pode ser descrita pela equação:
Σ MF = 0






