O movimento harmônico simples (MHS) é o movimento periódico produzido por um corpo ao redor da sua posição de repouso quando alteramos seu estado inicial ao aplicarmos uma força. Ele é caracterizado pela amplitude, período, frequência e velocidade angular. Nele não há forças dissipativas, em razão da conservação da energia mecânica.
Leia também: O que é movimento circular uniformemente variado?
Tópicos deste artigo
- 1 - Resumo sobre movimento harmônico simples (MHS)
- 2 - Características do movimento harmônico simples (MHS)
- 3 - Fórmulas do movimento harmônico simples (MHS)
- 4 - Exemplos de movimento harmônico simples (MHS)
- 5 - Energias no movimento harmônico simples (MHS)
- 6 - Exercícios resolvidos sobre movimento harmônico simples (MHS)
Resumo sobre movimento harmônico simples (MHS)
-
Movimento harmônico simples (MHS) é o movimento oscilatório realizado por um corpo em torno de sua posição de equilíbrio.
-
Esse movimento possui várias características que o descrevem: amplitude, período, frequência e velocidade angular.
-
A amplitude é a altura da onda.
-
O período é o tempo para completar uma oscilação.
-
A frequência é o número de oscilações feitas em um tempo específico.
-
A velocidade angular é a velocidade de um corpo durante um movimento circular.
-
O movimento harmônico simples é descrito por meio das funções horárias da posição, da velocidade e da aceleração.
-
Os casos de movimento harmônico simples são o oscilador massa-mola e o pêndulo simples.
-
O oscilador massa-mola é um sistema em que há um objeto preso a uma mola oscilando em torno da sua posição de equilíbrio, devido à compressão ou expansão da mola.
-
No oscilador massa-mola, a frequência e velocidade angular são proporcionais à constante da mola. Já o período é proporcional à massa do corpo conectado.
-
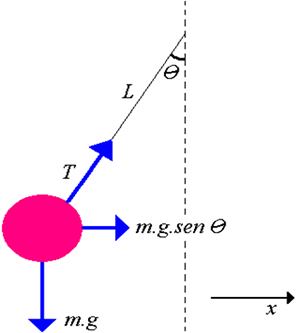
O pêndulo simples é um sistema em que há um objeto preso a um fio que oscila em torno da sua posição de equilíbrio, devido à força aplicada sobre ele.
-
No pêndulo simples, o período é proporcional ao comprimento do fio e inversamente proporcional à aceleração da gravidade.
-
No movimento harmônico simples, há conservação da energia mecânica.
-
As energias no movimento harmônico simples variam de acordo com a posição do objeto.
Características do movimento harmônico simples (MHS)
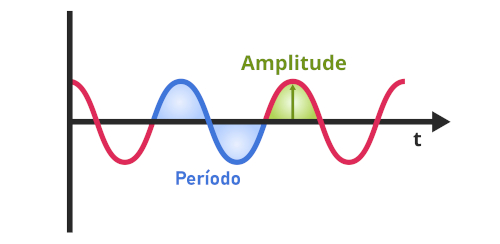
No movimento harmônico simples, há diversas características que descrevem o seu movimento, sendo elas a amplitude, período, frequência e velocidade angular. Na imagem, podemos ver algumas dessas características.
→ Amplitude no movimento harmônico simples (MHS)
A amplitude é a altura da onda, correspondendo à diferença entre a crista, o ponto mais alto que ela atingiu, e o ponto de equilíbrio, o ponto zero. Também pode ser a distância entre um dos pontos extremos do movimento e o ponto de equilíbrio.
→ Período no movimento harmônico simples (MHS)
O período é o tempo que leva para que o sistema em movimento harmônico simples complete uma oscilação, sendo o inverso da frequência.
→ Frequência no movimento harmônico simples (MHS)
A frequência é a quantidade de oscilações realizadas pelo sistema em movimento harmônico simples em um determinado tempo, sendo o inverso do período.
→ Velocidade angular no movimento harmônico simples (MHS)
A velocidade angular, também chamada de pulsação ou frequência angular, é a rapidez com que um corpo se desloca em um movimento circular.
Fórmulas do movimento harmônico simples (MHS)
→ Função horária da posição
\(x(t)=A\cdot cos(ω\ t+ϕ)\)
-
\(x(t)\) → posição em função do tempo, medida em metros \([m]\).
-
A → amplitude da onda, medida em metros \([m]\).
-
\(ω\ t+ϕ\) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s]\).
-
t → tempo, medido em segundos \([s]\).
-
\(ϕ\) → constante de fase.
Exemplo:
Qual a função horária da posição de um oscilador harmônico que possui amplitude de 1,5 metros, velocidade angular de 0,5 rad/s e constante de fase igual a \(\frac{\pi}{2}\)?
Resolução:
A função horária da posição de oscilador harmônico é dada pela equação:
\(x(t)=A\cdot cos(ω\ t+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(x(t)=1,5\cdot cos0\ (0,5\cdot t+\frac{π}2)\)
→ Função horária da velocidade
\(v(t)=-ω\cdot A\cdot sin\ (ω\ t+ϕ)\)
-
\(v(t)\) → velocidade em função do tempo, medida em metros \([m/s]\).
-
A → amplitude da onda, medida em metros \([m]\).
-
\(ω\ t+ϕ\) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s]\).
-
t → tempo, medido em segundos \([s]\).
-
\(ϕ\) → constante de fase.
Exemplo:
Qual a função horária da velocidade de um oscilador harmônico que possui amplitude de 3 metros, velocidade angular de 6 rad/s e constante de fase igual a \(\frac{\pi}{4}\)?
Resolução:
A função horária da velocidade de oscilador harmônico é dada pela equação:
\(v(t)=-ω\cdot A\cdot sin(ω\ t+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(v(t)=3\cdot cos(6\cdot t+\frac{π}4)\)
→ Função horária da aceleração
\(a(t)=ω^2\cdot A\cdot cos(ω\ t+ϕ)\)
-
\(a(t)\) → aceleração em função do tempo, medida em metros \([m/s^2]\).
-
A → amplitude da onda, medida em metros \([m]\).
-
\(ω\ t+ϕ \) → fase do movimento.
-
ω → velocidade angular, medida em \([rad/s]\).
-
t → tempo, medido em segundos \([s]\).
-
\(ϕ \) → constante de fase.
Pode ser representada também por:
\(a(t)=ω^2\cdot x(t)\)
-
\(a(t)\) → aceleração em função do tempo, medida em metros \([m/s^2]\).
-
ω → velocidade angular, medida em \([rad/s]\).
-
\(x(t)\) → posição em função do tempo, medida em metros \([m]\).
Exemplo:
Qual a função horária da aceleração de um oscilador harmônico que possui amplitude de 2,5 metros, velocidade angular de 4 rad/s e constante de fase igual a π?
Resolução:
A função horária da aceleração do oscilador harmônico é dado pela equação:
\(a(t)=ω^2\cdot A\cdot cos(ω\ t+ϕ)\)
Substituindo os valores dados no enunciado, obteremos a função para esse caso:
\(x(t)=2,5\cdot cos(4+π)\)
→ Período
\(T=\frac{1}f\)
-
T → período, medido em segundos \([s]\).
-
f → frequência, medida em Hertz \([Hz]\).
Pode ser representado também por:
\(T=\frac{∆t}n\)
-
T → período, medido em segundos \([s]\).
-
\(∆t\) → variação de tempo, medida em segundos \([s]\).
-
n → número de oscilações.
→ Frequência
\(f=\frac{1}T\)
-
f → frequência, medida em Hertz \([Hz]\).
-
T → período, medido em segundos \([s]\).
Pode ser representada também por:
\(f=\frac{n}{∆t}\)
-
f → frequência, medida em Hertz \([Hz]\).
-
n → número de oscilações.
-
\(∆t\) → variação de tempo, medida em segundos \([s]\).
→ Velocidade angular
\(ω=2\cdotπ\cdot f\)
-
\(ω\) → velocidade angular, medida em \([rad/s]\).
-
f → frequência, medida em Hertz \([Hz]\).
Pode ser representada também por:
\(ω=\frac{2π}T\)
-
\(ω\) → velocidade angular, medida em \([rad/s]\).
-
T → período, medido em segundos \([s]\).
Veja também: Relação entre as velocidades, o período e a frequência no movimento circular uniforme (MCU)
Exemplos de movimento harmônico simples (MHS)
Os principais exemplos de movimento harmônico simples são os osciladores harmônicos e os pêndulos simples, como veremos a seguir.
→ Oscilador massa-mola
O oscilador massa-mola, também chamado de oscilador harmônico, é um sistema composto por um corpo conectado a uma mola que ao deformar, seja comprimindo ou alongando a mola, passa a oscilar em torno da sua posição de equilíbrio (ponto em que está parado) em razão da força elástica exercida pela mola, como podemos ver na imagem abaixo:
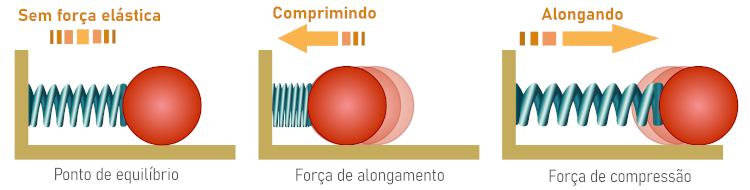
No oscilador harmônico, o material da mola e a massa do corpo associado interferem na rapidez da oscilação. Quanto mais rígida for a mola, mais rápida será a velocidade e a frequência de oscilação, já que essas grandezas são proporcionais à constante da mola. Contudo, o período de oscilação é proporcional à massa do objeto conectado, sendo que quanto mais leve for, mais rápido será seu período.
Em razão disso, podemos calcular o período, a frequência e a velocidade angular do oscilador massa-mola por meio das fórmulas a seguir.
◦ Período do oscilador massa-mola
\(T=2π\cdot\sqrt{\frac{m}k}\)
-
T → período, medido em segundos \([s]\).
-
m → massa do corpo, medida em quilogramas \([kg]\).
-
k → constante da mola, medida em \([N/m]\).
◦ Frequência do oscilador massa-mola
\(f=\frac{1}{2π}\cdot\sqrt{\frac{k}{m}}\)
-
f → frequência, medida em Hertz \([Hz]\).
-
k → constante da mola, medida em \([N/m]\).
-
m → massa do corpo, medida em quilogramas \([kg]\).
◦ Velocidade angular do oscilador massa-mola
\(ω=\sqrt{\frac{k}{m}}\)
-
\(ω\) → velocidade angular, medida em \([rad/s]\).
-
k → constante da mola, medida em \([N/m]\).
-
m → massa do corpo, medida em quilogramas \([kg]\).
→ Pêndulo simples
O pêndulo simples é um sistema constituído por um corpo preso a um fio que não se estende. Ao ser aplicada uma força, ele passa a oscilar, na existência de um campo gravitacional, como podemos ver na imagem a seguir:
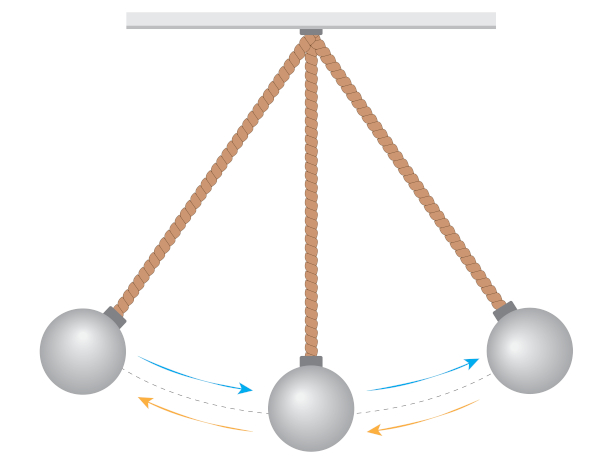
No pêndulo simples, o comprimento do fio e a aceleração da gravidade do local influenciam na rapidez da oscilação. Quanto maior for o comprimento do fio, maior será o seu período de oscilação. Já quanto maior for a aceleração da gravidade em que foi colocado o pêndulo, menor será o seu período de oscilação.
Em razão disso, podemos calcular o período e a frequência do pêndulo simples por meio das fórmulas a seguir.
◦ Período do pêndulo simples
\(T=2\cdotπ\cdot\sqrt{\frac{l}g}\)
-
T → período, medido em segundos \([s]\).
-
l → comprimento do fio, medido em metros \([m]\).
-
g → aceleração da gravidade, medida em \([m/s^2]\).
◦ Frequência do pêndulo simples
\(f=\frac{1}{2\cdotπ}\cdot\sqrt{\frac{g}l}\)
-
f → frequência, medida em Hertz \([Hz]\).
-
g → aceleração da gravidade, medida em \([m/s^2]\).
-
l → comprimento do fio, medido em metros \([m]\).
Energias no movimento harmônico simples (MHS)
No movimento harmônico simples, não há forças dissipativas, como a força de atrito e a força de arraste, já que a energia mecânica é conservada. A energia cinética é convertida em energia potencial ou vice-versa.
Em razão disso, começamos com a fórmula da conservação de energia mecânica para calcular as energias no MHS, que é dada por:
\(E_m=E_c+E_{pel}\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
\(E_c\) → energia cinética, medida em Joule \([J]\).
-
\(E_{pel}\) → energia potencial elástica, medida em Joule \([J]\).
Contudo, essa fórmula sofrerá alterações de acordo com a posição em que o objeto se encontra, como veremos a seguir.
→ Energia de um objeto na posição de equilíbrio
Quando o objeto estiver na posição de equilíbrio, não há energia potencial elástica, já que a posição está no ponto zero, como podemos ver na imagem abaixo.

Como \(x=0\), a velocidade será máxima, portanto a energia mecânica é dada pela fórmula:
\(E_m=\frac{m\cdot v_{máx}^2}2\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
m → massa, medida em quilograma \([kg]\).
-
\(v_{máx}\) → velocidade máxima, medida em \([m⁄s]\).
→ Energia de um objeto no ponto de máxima compressão
Quando o objeto estiver na posição de máxima compressão, em que \( x=-A\), não há energia cinética, já que a velocidade é igual a zero, como podemos ver na imagem abaixo.
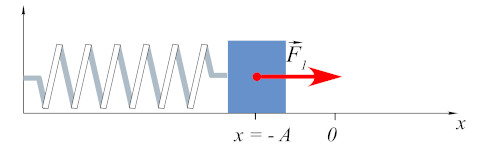
Como \(v=0\), a posição será de máxima compressão, portanto a energia mecânica é dada pela fórmula:
\(E_m=\frac{k\cdot x_{máx}^2}2\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
k → constante da mola, medida em \([N/m]\).
-
\(x_{máx}\) → deformação máxima da mola, medida em metros \([m]\).
Se chamarmos o ponto de máxima compressão de \(-A\), a fórmula muda para:
\(E_m=\frac{k\cdot A^2}2\)
-
Em → energia mecânica, medida em Joule \([J]\).
-
k → constante da mola, medida em \([N/m]\).
-
A → deformação máxima da mola, medida em metros \([m]\).
→ Energia de um objeto no ponto de máxima elongação
Quando o objeto estiver na posição de máxima elongação, em que \(x=A\), não há também energia cinética, pois a velocidade é igual a zero, como podemos ver na imagem abaixo.

Como \(v=0\), a posição será de máxima elongação, portanto a energia mecânica é dada pela fórmula:
\(E_m=\frac{k\cdot x_{máx}^2}2\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
k → constante da mola, medida em \( [N/m]\).
-
\(x_{máx}\) → elongação máxima da mola, medida em metros \( [m]\).
Se chamarmos o ponto de máxima elongação de A, a fórmula muda para:
\(E_m=\frac{k\cdot A^2}2\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
k → constante da mola, medida em \([N/m]\).
-
A → elongação máxima da mola, medida em metros \([m]\).
→ Energia em um ponto qualquer
Quando o objeto estiver em um ponto qualquer que não seja nos pontos máximos e no ponto de equilíbrio, a energia mecânica é dada pela somatória entre a energia cinética e a energia potencial elástica:
\(E_m=E_c+E_{pel}\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
\(E_c\) → energia cinética, medida em Joule \([J]\).
-
\(E_{pel}\) → energia potencial elástica, medida em Joule \([J]\).
Então, a energia mecânica de um objeto em uma posição qualquer que descreve um movimento harmônico simples é:
\(E_m=\frac{m\cdot v^2}2+\frac{k\cdot x^2}2\)
-
\(E_m\) → energia mecânica, medida em Joule \([J]\).
-
m → massa, medida em quilograma \([kg]\).
-
v → velocidade, medida em \([m/s]\).
-
k → constante da mola, medida em \([N/m]\).
-
x → elongação ou deformação da mola, medida em metros \([m]\).
Saiba mais: Energia potencial elétrica — a energia relacionada à interação entre corpos eletricamente carregados
Exercícios resolvidos sobre movimento harmônico simples (MHS)
Questão 1
(Unitau) Um corpo de massa m, ligado a uma mola de constante elástica k, está animado de um movimento harmônico simples. Nos pontos em que ocorre a inversão no sentido do movimento:
A) são nulas a velocidade e a aceleração.
B) são nulas a velocidade e a energia potencial.
C) o módulo da aceleração e a energia potencial são máximas.
D) a energia cinética é máxima e a energia potencial é mínima.
E) a velocidade, em módulo, e a energia potencial são máximas.
Resolução:
Alternativa C
Nos pontos em que ocorre a inversão no sentido do movimento harmônico simples, há uma velocidade nula que ocasiona uma energia cinética nula. Em razão disso, a energia potencial é máxima, assim como a aceleração.
Questão 2
(Osec) Um móvel executa um movimento harmônico simples de equação
\(x(t)=8\cdot cos(\frac{π}8\cdot t)\)
Em que t é dado em segundos e x em metros. Após 2,0 s, a elongação do movimento é:
A) zero
B) 2,0 m
C) 3,5 m
D) 5,7 m
E) 8,0 m
Resolução:
Alternativa D
A elongação do movimento será dada pela substituição do tempo de 2 segundos na sua equação:
\(x(t)=8\cdot cos(\frac{π}8\cdot 2)\)
\(x(t)=8\cdot cos(\frac{π}4)\)
\(x(t)=8\cdot cos(0,25\cdot\pi)\)
\(x(t)=8\cdot0,707\)
\(x(t)=5,7\ m\)
Quetão 3
Qual a velocidade angular e o período de onda harmônica simples de frequência 300 Hz? Considere π = 3.
A) 1900 rad/s e 0,0034 s
B) 1100 rad/s e 0,0039 s
C) 1300 rad/s e 0,0035 s
D) 1800 rad/s e 0,0033 s
E) 1700 rad/s e 0,0027 s
Resolução:
Alternativa D
Calcularemos a velocidade angular da onda usando a fórmula:
\(ω=2\cdot π\cdot f\)
\(ω=2\cdot3\cdot300\)
\(ω=1800\ rad/s\)
Já o período é calculado usando a fórmula:
\(T=\frac{1}f\)
\(T=\frac{1}{300}\)
\(T≈0,0033\ s\)
Assim, a velocidade angular dessa onda é de \(1800\ \frac{rad}s\), e o seu período é de 0,0033 s.