Como sabemos, um dos objetivos da Física é realizar o estudo do movimento. Agora vamos dar mais atenção ao estudo do movimento relacionado com sua rotação. Vemos rotações em quase todas as máquinas, usamos rotações toda vez que abrimos uma tampa de rosca, quando vamos ao parque de diversões, etc. Podemos dizer que a rotação é o segredo de muitas atividades cotidianas.
Analisaremos a rotação de um corpo rígido em torno de um eixo fixo. Um corpo rígido é um corpo que pode girar com todas as partes ligadas rigidamente e sem mudar de forma.
Deslocamento angular
De acordo com a figura abaixo, representamos um corpo que se deslocou do ponto A até o ponto B sobre uma circunferência de centro O e raio R. O comprimento ΔS do arco (AB) ̂ é o espaço percorrido pela partícula, e o ângulo central ΔӨ oposto ao arco (AB) ̂ é o deslocamento angular.
∆θ = θB - θA
.jpg)
Deslocamento angular
Velocidade angular
.jpg)
Partícula em movimento circular
De acordo com a figura, supomos que, num intervalo de tempo Δt, uma partícula em movimento circular execute um deslocamento angular ∆θ. A velocidade angular média (ωm) da partícula nesse intervalo de tempo é definida por:
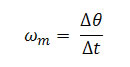
No Sistema Internacional, a unidade de velocidade angular é o rad/s, mas frequentemente são também usadas rev/s e rev/min.
A velocidade angular (instantânea) ω é definida por meio de um limite quando o tempo Δt tende a zero. Assim, temos:
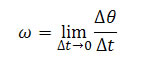
Onde ∆θ é o deslocamento angular e ∆t é a variação do tempo.










