A potência é fruto da razão entre a energia consumida em uma atividade e o tempo gasto para a realização dela, portanto:
Potência = Energia
Tempo
Como a unidade de energia é o joule (J) e a unidade de tempo é o segundo (s), a potência é dada em joules por segundo (J/s), unidade que é chamada de watt (W) em homenagem ao cientista escocês James Watt, responsável pelo melhoramento de motores a vapor.
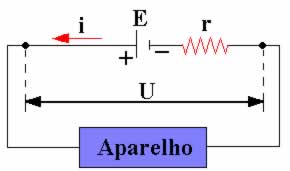
Em se tratando de equipamentos elétricos, a definição de potência é a mesma, mas a sua determinação é feita por meio do produto da diferença de potencial (V) à qual se submete o aparelho pela corrente elétrica (i) que o percorre, sendo assim, temos:
P = V.i
Ainda nesse caso a potência é fornecida na unidade watt (W).
-
Potência dissipada por um resistor
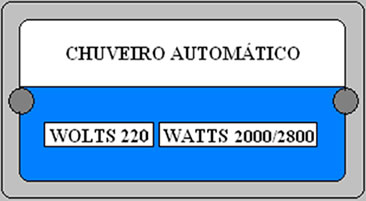
Alguns aparelhos elétricos cumprem a função de apenas transformar energia elétrica em energia térmica (calor), processo que é chamado de efeito Joule. Equipamentos como ferro elétrico, aquecedores e chuveiro elétrico fazem a conversão de energia elétrica em calor por meio de um resistor.

Transformação de energia elétrica em calor em uma churrasqueira elétrica
Nesse caso, pode-se deduzir duas equações para determinar a potência consumida por tais resistores. Para a determinação dessas equações, vamos partir da definição da potência elétrica dada acima:
P = V.i
Por causa da Primeira lei de Ohm, sabemos que a diferença de potencial é o produto da resistência do resistor pela corrente elétrica:
V = R . i
Substituindo uma equação na outra, temos:
P = V . i
P = R . i . i
P = R . i2
Isolando a corrente elétrica na primeira lei de Ohm, temos:
i = V/R
Voltando à equação-base da potência elétrica, ainda é possível escrever:
P = V . i
P = V . V
R
P = V2
R
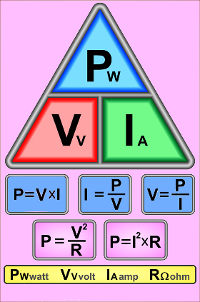
A imagem abaixo pode auxiliar na memorização das equações para potência.