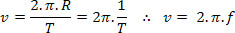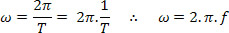Em nossos estudos vimos que estamos cercados de exemplos de movimento cujas trajetórias são circulares. É o caso, por exemplo, do movimento de um ponto em um disco, a roda de uma motocicleta, uma roda gigante, etc. Sabemos que para descrever os movimentos circulares, é necessário definir novas grandezas cinemáticas, como deslocamento angular, velocidade angular e aceleração angular – isto de maneira análoga ao que fizemos nas grandezas escalares.
Tratando-se de um movimento circular, definimos Período (T) como sendo o menor intervalo de tempo para o movimento repetir-se com as mesmas características. Para o movimento circular uniforme, período é o tempo gasto para que o móvel efetue uma volta completa na circunferência.
Definimos a frequência (f) como sendo o número de vezes que um fenômeno periódico se repete na unidade de tempo. Para o movimento circular uniforme, ela corresponde ao número de voltas que o móvel realiza por unidade de tempo. Partindo das definições de período e frequência citadas a cima, podemos estabelecer a relação entre essas duas grandezas da seguinte maneira:
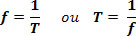
Relação entre as velocidades, o período e a frequência no MCU
Não somente podemos fazer a relação entre período e frequência, como citamos acima, mas também podemos estabelecer uma simples e fácil relação entre a velocidade angular de um objeto que descreve um movimento circular, e o seu período.
Quando falamos em uma volta completa no MCU, estamos nos referindo, na verdade, ao deslocamento angular do móvel. Esse descolamento pode ser representado pela letra (Δθ), sendo seu valor igual a 2π radianos; e o intervalo de tempo (Δt), igual ao período (T).
Como sabemos que a velocidade angular média é igual à velocidade angular instantânea, podemos escrever:
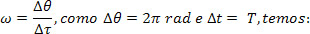
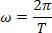
A equação acima é a equação angular em função do período no MCU.
Dessa relação, podemos obter a velocidade linear (v), pois já sabemos qual a relação entre ela e a velocidade angular (ω). Como:
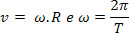
Teremos:
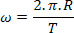
Velocidade linear em função do período no MCU
Observe, na equação acima, que 2.π.R é o comprimento da circunferência descrita pelo móvel, enquanto T é o período do movimento. Também é possível obter, pelo fato de se conhecer a relação entre período e frequência, a velocidade angular e linear do MCU.
Sendo assim, a velocidade angular e linear podem ser relacionadas com a frequência da seguinte forma: