Para analisar o movimento de um objeto que está girando, basta observar um ponto desse objeto, pois todos os pontos dele estão girando com o mesmo período. Observe a figura acima, na qual temos uma caneta girando sobre a mesa. A ponta faz um giro completo no mesmo intervalo de tempo que um ponto perto do centro. Essa propriedade é útil, pois permite descrever a rotação de um objeto complexo, olhando-se para um ponto qualquer dele.
Observe um ponto qualquer de um disco que gira. A posição desse ponto muda com o tempo. Pode-se localizar o ponto, conhecendo o ângulo de rotação θ que ele faz com o eixo x, bem como a distância entre o eixo de rotação e o ponto considerado. O ângulo é medido a partir do eixo x, no sentido anti-horário, ou seja, no sentido oposto ao dos ponteiros do relógio.
Vamos convencionar o sentido anti-horário como o sentido positivo para o deslocamento angular. Se um corpo gira no sentido horário, ele está girando no sentido negativo do nosso sistema.
Vamos sempre usar, como medida de ângulo, o radiano. Lembre-se de que uma volta completa corresponde a um ângulo de 360º ou 2π radianos.
Consideremos o movimento de um ponto no disco que gira, como na figura abaixo. Vemos que no instante t1, o ponto está na posição 1; e que no instante t2 ele está na posição 2. Na posição 1, o ângulo que ele faz com o eixo x é θ1 e na posição 2, é o ângulo θ2.
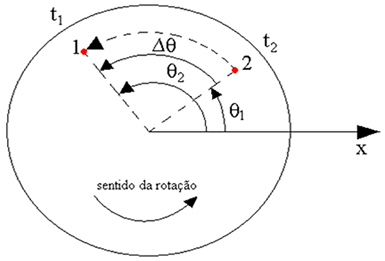
No intervalo de tempo Δt = t2 – t1, ele percorreu o ângulo Δθ = θ2 – θ1. Vamos definir a velocidade angular desse ponto como a variação do ângulo percorrido no intervalo de tempo. Para converter rpm em rad/s, utilizamos a relação:
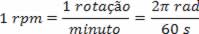
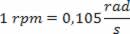
A letra grega ω (ômega minúsculo) representa a velocidade angular. Dessa forma, temos:
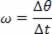
A unidade de velocidade angular é dada em radianos/segundo (rad/s). Apesar de ser pouco usada, também podemos medir a velocidade angular em rotações por minuto (rpm). Podemos calcular a velocidade angular, conhecendo o período T. Sabemos que o ponto faz uma volta completa, Δθ = 2π radianos em um período, ou seja, o intervalo de tempo Δt = T.
Matematicamente temos:
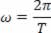
Ou, em termos de frequência f,
ω=2πf
Se o ponto parte de uma posição θ0, em t = 0, podemos calcular sua nova posição angular no instante t usando:
θ=θ0+ω.t






