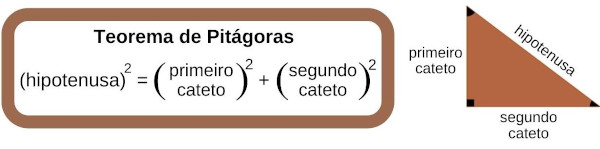
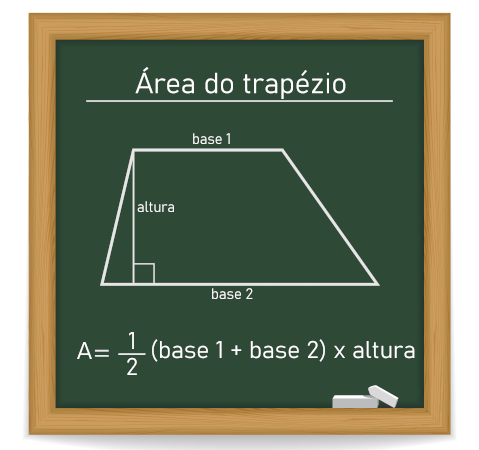
O triângulo é uma das formas geométricas mais importantes, apresentando aplicações em diversas áreas do conhecimento, como engenharia e arquitetura. Devido à sua rigidez, o triângulo é usado em estruturas metálicas e madeiramento de telhados, garantindo segurança nas construções. É uma figura que sempre intrigou filósofos e matemáticos de todas as épocas, que acabaram realizando vários estudos sobre esse polígono com o menor número de lados. Hoje sabemos que a soma dos ângulos internos de qualquer triângulo é 180o, que a soma das medidas de dois de seus lados é maior ou igual à medida do terceiro, e que sua área equivale à metade do produto da base pela altura.
Vamos determinar a fórmula para o cálculo da área de um triângulo equilátero em função apenas da medida de seus lados.
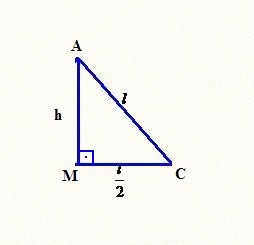
Dessa forma, considere um triângulo equilátero de lado l, como mostra a figura.
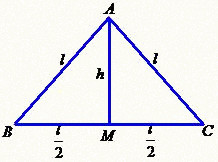
Sabemos que a área de qualquer triângulo é dada por:
![]()
Vamos chamar a base de b e a altura de h. No triângulo equilátero, b = l e a altura é, ao mesmo tempo, mediatriz e bissetriz. Dessa forma, podemos utilizar o teorema de Pitágoras para determinar a altura em função do lado l.
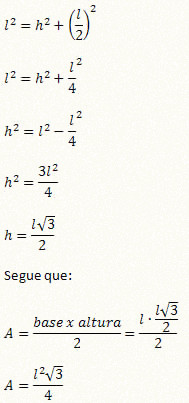
Que é a fórmula para o cálculo da área do triângulo equilátero em função apenas da medida do lado.
Exemplo 1. Qual a área de um triângulo equilátero de lado 5 cm?
Solução: Sabemos que l = 5cm. Assim,
![]()
Exemplo 2. Um triângulo equilátero possui área de 16√3 cm2. Determine a medida do lado desse triângulo.
Solução: Temos que A = 16√3 cm2. Logo,
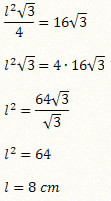
Portanto, os lados desse triângulo medem 8 cm.
Exemplo 3. Determine a medida da altura de um triângulo equilátero de área 25√3 cm2.
Solução: Podemos determinar a altura do triângulo equilátero se as medidas de seus lados forem conhecidas. Assim, vamos encontrar a medida do lado utilizando a área que foi dada pelo exercício.

Aproveite para conferir nossas videoaulas relacionadas ao assunto: