Circunferências e círculos são figuras muito parecidas, mas com uma diferença muito importante: a circunferência é a borda do círculo. Isso é causa de muitas confusões e repercute diretamente tanto na definição dessas duas figuras geométricas quanto em algumas de suas propriedades.
Para acabar com as dúvidas em relação a essas duas figuras, vamos discutir suas definições e propriedades. Esperamos, com isso, demonstrar suas diferenças básicas.
Definição de circunferência
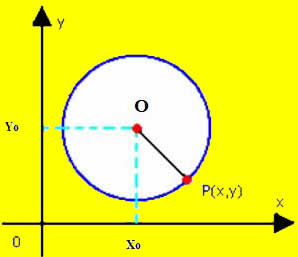
Dados um ponto C (chamado centro da circunferência) do plano e uma distância r (chamada raio da circunferência), uma circunferência é o conjunto de pontos desse mesmo plano cuja distância até o ponto C é igual a r. Isso é equivalente a dizer que, dado o ponto C, qualquer ponto P cuja distância até C seja igual a r pertencerá à circunferência.
Por exemplo, se fixados a distância em 4 centímetros e o ponto C (ilustrados na imagem a seguir), o conjunto de todos os pontos que possuem 4 centímetros de distância do ponto C será a circunferência em destaque.
Dessa maneira, considere os pontos A e B pertencentes a uma circunferência de centro C. A distância entre A e C é representada por dAC, e a distância entre B e C é representada por dBC. Nessas circunstâncias, dAC = dBC = r.
Digamos que um ponto P está no interior da circunferência e um ponto S está no exterior dessa figura. Nesse caso, os pontos P e S não pertencem à circunferência, pois:
dPC < r
dSC > r
Definição de círculo
O círculo é uma figura geométrica formada por uma parte de um plano que é limitada por uma circunferência. Em outras palavras, dados um ponto C (chamado centro do círculo) e uma distância r (chamada raio do círculo), o círculo é o conjunto de pontos cuja distância até C é igual ou menor que r. Matematicamente, o ponto P pertencerá ao círculo se:
dPC ≤ r
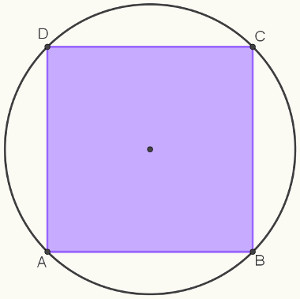
Sendo assim, na figura a seguir, os pontos A, B, C e P pertencem ao círculo, que é toda a seguinte figura em verde. Já o ponto D não pertence ao círculo, pois está em seu exterior.
.jpg)
Portanto, de acordo com as duas definições acima, a circunferência possui os mesmos pontos que a borda de um círculo. Já o círculo possui todos os pontos internos de uma circunferência. Logo, o círculo é uma região plana, e a circunferência é uma linha.
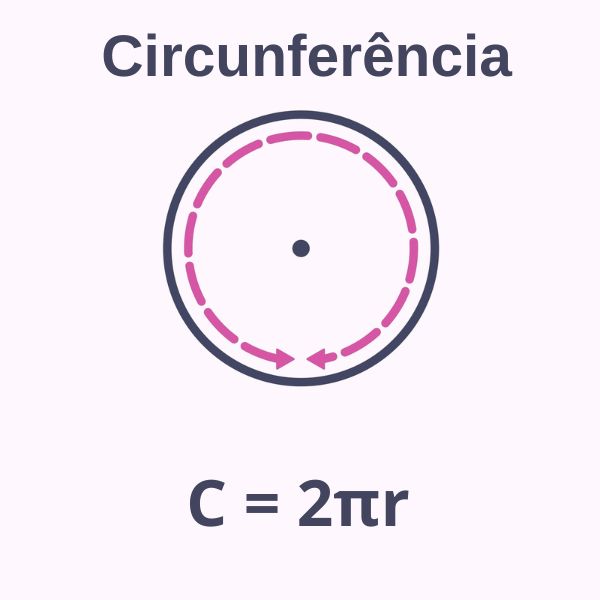
Perímetro
O perímetro é uma medida do comprimento da borda de uma figura geométrica. Assim, é possível calcular o perímetro tanto do círculo quanto da circunferência usando a seguinte fórmula:
C = 2·π·r
Em que C = comprimento ou perímetro; r = raio do círculo ou circunferência em questão; e π é uma constante irracional comumente arredondada para 3,14.
Isso acontece porque toda circunferência é o perímetro de um círculo com centro e raio iguais.
Área
Ao passo que o comprimento pode ser calculado tanto sobre o círculo quanto sobre a circunferência, a área da circunferência não pode ser calculada, diferentemente do círculo que pode ter essa medida calculada.
Assim, a área é uma medida referente à superfície ocupada por uma figura geométrica, isto é, ela depende da quantidade de plano que essa figura ocupa. A área é, portanto, a medida referente às regiões planas.
Entretanto, sempre que a “área da circunferência” for citada, poderemos entender como a área do círculo limitado por aquela circunferência. Não há problemas em usar essa expressão.
A área do círculo pode ser calculada usando a seguinte fórmula:
A = π·r2
Em que A = área do círculo, r = raio do círculo e π é a mesma constante do comprimento ou perímetro.


.jpg)