Existe uma propriedade que pode ser usada para verificar a existência de um triângulo de acordo com as medidas dos seus lados. Essa propriedade é conhecida como condição de existência de um triângulo. Para compreendê-la bem, é importante conhecer seus fundamentos.
Fundamentos
Suponha que alguém queira usar três segmentos de reta (a, b e c) para construir um triângulo. A ideia dessa pessoa é simples: unir as pontas desses segmentos e verificar a figura formada. Imagine que as medidas são: a = 12 cm, b = 6 cm e c = 9 cm. Observe o triângulo que será construído:
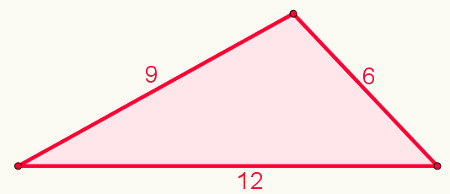
Uma alternativa para a construção desse triângulo é fixar as extremidades dos segmentos menores com as da base e depois girar esses segmentos menores até que as suas extremidades livres toquem-se e formem o terceiro vértice do triângulo.
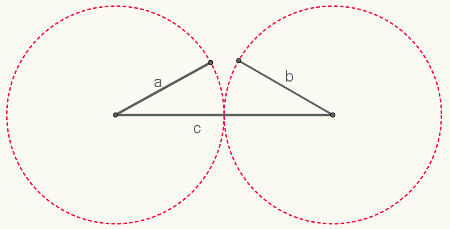
Seguindo essa mesma estratégia, tentaremos construir um triângulo com segmentos que valem: a = 12 cm, b = 5 cm e c = 6 cm.
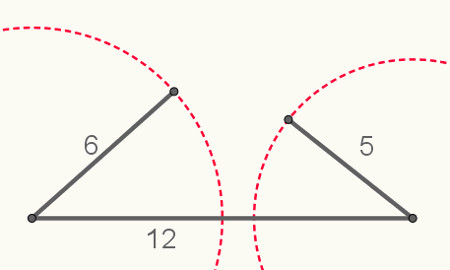
Não é possível construir um triângulo com essas medidas, pois não existe ponto de encontro nas trajetórias dos segmentos, como foi mostrado por meio de duas circunferências na imagem anterior.
Quais serão, portanto, as medidas de segmentos que podem gerar triângulos e as medidas que não podem?
Condição de existência de um triângulo
A condição para que esses segmentos formem um triângulo é a seguinte: sempre que a soma das medidas dos segmentos que estão sendo girados for maior que a medida do terceiro segmento, é possível construir um triângulo. Para verificar sua existência, portanto, devemos somar os segmentos dois a dois e verificar se essa soma é maior que o terceiro segmento. Matematicamente:
Em qualquer triângulo, a soma das medidas de dois lados é sempre maior que a medida do terceiro.
Dado um triângulo cujos segmentos medem a, b e c, esse triângulo somente existirá se:
a + b < c
a + c < b
b + c < c
Esse conjunto de inequações é conhecido como desigualdade triangular. Existe uma maneira de simplificar essa propriedade. Basta calcular a soma dos lados menores e compará-la com o lado maior. Suponha que a e b são os lados menores. As somas a + c e b + c sempre serão maiores que b e que a, respectivamente. Assim, nessa hipótese, basta calcular uma soma, que é a + b, para compará-la com o terceiro lado. Assim sendo, basta comparar a soma dos lados menores com o lado maior na desigualdade triangular.
Como última observação, um triângulo cuja soma dos lados menores é igual à medida do lado maior também não pode existir. Observe a figura a seguir:
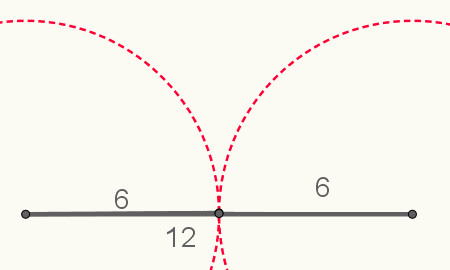
Exemplo
Um engenheiro precisa construir uma piscina triangular e quer que suas dimensões sejam: 5 m x 2 m x 1 m. Será possível construir essa piscina?
Observe que a soma dos lados menores é:
2 + 1 = 3
Observe também que 3 < 5; logo, é impossível construir essa piscina.