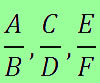Números racionais são os números que podem ser representados como uma fração em que o numerador e o denominador são inteiros. As frações, as dízimas periódicas e os números com uma quantidade finita de casas decimais são exemplos de números racionais. Eles são utilizados para indicar partes de um inteiro, como meia xícara de açúcar, um terço de pizza e dois quintos de chocolate.
Leia também: Números reais — a união dos números racionais e dos números irracionais
Tópicos deste artigo
- 1 - Resumo sobre números racionais
- 2 - Videoaula sobre números racionais
- 3 - O que são números racionais?
- 4 - Operações com números racionais
- 5 - Números racionais e dízimas periódicas
- 6 - Conjunto dos números racionais
- 7 - Subconjuntos dos números racionais
- 8 - Diferenças entre números racionais e irracionais
- 9 - Exercícios resolvidos sobre números racionais
Resumo sobre números racionais
- Um número que pode ser escrito como uma fração em que o numerador e o denominador são inteiros é chamado de racional.
- As operações com números racionais seguem alguns critérios específicos.
- As dízimas periódicas — números com infinitas casas decimais periódicas — são exemplos de números racionais.
- O conjunto dos números racionais é representado pela letra Q.
- O conjunto dos números naturais (N) e o conjunto dos números inteiros (Z) são subconjuntos de Q.
- Os números que não podem ser expressos por frações com numerador e denominador inteiros são chamados de irracionais.
Videoaula sobre números racionais
O que são números racionais?
Os racionais são os números que podem ser escritos na forma \(\frac{{a}}{{b}},\), em que a e b são números inteiros e b≠0. Todos os números com quantidade finita de casas decimais e com quantidade infinita e periódica de casas decimais são racionais. Veja exemplos:
2 é racional, pois \(2=\frac{2}{1}\)
0,25 é racional, pois \(0,25=\frac{1}{4}\)
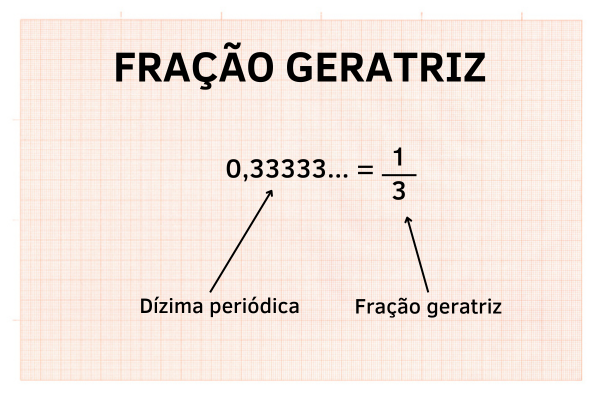
0,3333... é racional, pois \(0,3333... = \frac{1}{3}\)
-6 é racional, pois \(-6=\frac{-6}{1}\)
\(\frac{1}{10}\) é racional
Operações com números racionais
Vejamos como realizar as quatro operações matemáticas básicas (adição, subtração, multiplicação e divisão) com números racionais na representação fracionária. Para isso, vamos considerar operações entre os números racionais \(\frac{a}{b} e \frac{c}{d}, \), em que \( b\neq0\) e \(d\neq0\).
→ Adição entre números racionais
\(\frac{a}{b}\ +\ \frac{c}{d}\ =\ \frac{a.d\ +\ c.b}{b.d}\)
Veja um exemplo:
\(\frac{3}{5}+\frac{2}{9}=\frac{3.9\ +\ 2.5}{5.9}=\frac{27+10}{45}=\frac{37}{45}\)
→ Subtração entre números racionais
\(\frac{a}{b}\ -\ \frac{c}{d}\ =\ \frac{a.d\ -\ c.b}{b.d}\)
Veja um exemplo:
\(\frac{4}{3}-\frac{1}{2}=\frac{4.2\ -\ 1.3}{3.2}=\frac{8-3}{6}=\frac{5}{6}\)
→ Multiplicação entre números racionais
\(\frac{a}{b}\cdot\frac{c}{d}\ =\ \frac{a\ \cdot\ c}{b\ \cdot\ d}\)
Veja um exemplo:
\(\frac{8}{10}\cdot\frac{7}{4}=\frac{8\ \cdot\ 7}{10\ \cdot\ 4}=\frac{56}{40}\)
→ Divisão entre números racionais
\(\frac{a}{b}\div\frac{c}{d}=\frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}\)
Veja um exemplo:
\(\frac{4}{9}\div\frac{1}{3}=\frac{4}{9}\cdot\frac{3}{1}=\frac{4\cdot3}{9\cdot1}=\frac{12}{9}\)
Números racionais e dízimas periódicas
As dízimas periódicas são números cuja parte decimal é infinita e periódica. Toda dízima periódica pode ser escrita na forma de uma fração em que o numerador e o denominador são números inteiros. Assim, as dízimas periódicas são números racionais. Veja os exemplos:
- A dízima periódica 1,3333... é racional, pois \(1,3333\ldots=\frac{4}{3}\).
- A dízima periódica 2,4444... é racional, pois \(2,4444\ldots=\frac{22}{9}\).
Conjunto dos números racionais
O conjunto dos números racionais é simbolizado pela letra Q. Formalmente, ele é descrito da seguinte maneira:
\(Q=\ \left\{\ \frac{a}{b},a\in Z,b\in Z^\ast\right\}\)
Subconjuntos dos números racionais
Os principais subconjuntos dos números racionais são:
- N: conjunto dos números naturais.
- Z: conjunto dos números inteiros.
- Q*: conjunto dos números racionais não nulos.
- Q+: conjunto dos números racionais positivos.
- Q-: conjunto dos números racionais negativos.
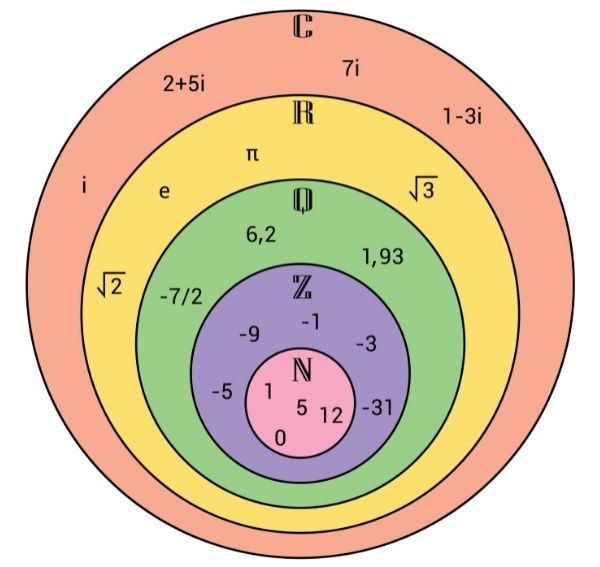
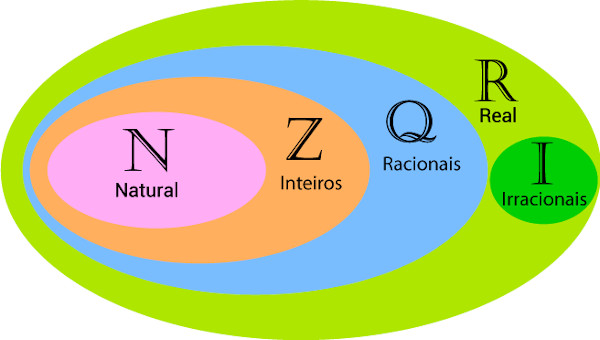
Em particular, vamos observar a relação de inclusão entre os conjuntos N, Z e Q. Lembre-se de que:
\(N=\{\ 1,\ 2,\ 3,\ 4,\ 5\ldots\}\)
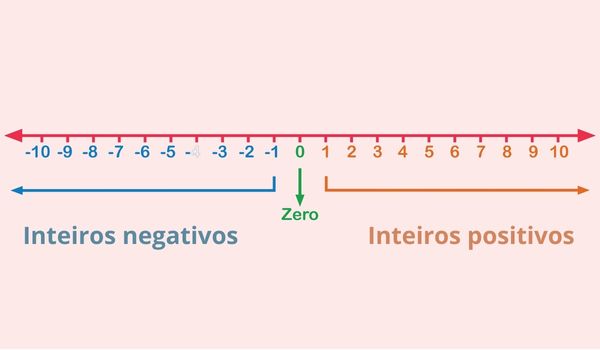
\(Z=\{\ldots\ -3,-2,-1,\ 0,\ 1,\ 2,\ 3\ldots\}\)
\(Q=\ \left\{\ \frac{a}{b},a\in Z,b\in Z^\ast\right\}\)
Assim, \(N\subset Z\subset Q\).
Veja também: Quais são os subconjuntos dos números naturais?
Diferenças entre números racionais e irracionais
- Números racionais: podem ser expressos por frações em que o numerador e o denominador são inteiros. Exemplos:
\(0,2=\ \frac{1}{5}\)
\(1,875=\ \frac{15}{8}\)
\(2,3333\ldots=\ \frac{7}{3}\)
- Números irracionais: são exatamente o contrário dos racionais, ou seja, não podem ser escritos como frações com numerador e denominador inteiros. Podemos reconhecer um número irracional analisando sua parte decimal. Todo número irracional possui infinitas casas decimais não periódicas. Exemplos:
\(\sqrt2=1,41421356237\ldots\)
\(\sqrt3=1,73205080756\ldots\)
\(\pi=3,14159235358\ldots\)
Exercícios resolvidos sobre números racionais
Questão 1
Leia as afirmações abaixo e classifique cada uma em V (verdadeira) ou F (falsa).
I. O número \(\frac{1}{5}\) é irracional.
II. As dízimas periódicas são números racionais.
III. O número 0,3789 é racional.
A sequência correta, de cima para baixo, é:
A) V-V-V
B) F-F-F
C) F-V-F
D) V-F-V
E) F-V-V
Resolução:
Alternativa E
I. O número \(\frac{1}{5}\) é irracional. (falso)
\(\frac{1}{5} \) é uma fração com numerador e denominador inteiros; consequentemente, é um número racional.
II. As dízimas periódicas são números racionais. (verdadeiro)
Toda dízima periódica pode ser expressa por uma fração com numerador e denominador inteiros.
III. O número 0,3789 é racional. (verdadeiro)
\(0,3789=\frac{3789}{10000}\)
Questão 2
Considere as afirmações a seguir.
I. Todo número negativo é irracional.
II. Z⊂I
III. \(\sqrt4\) é um número racional.
Está correto o que se afirma em:
A) I apenas.
B) I e II apenas.
C) II e III apenas.
D) III apenas.
E) I, II e III.
Resolução:
Alternativa D
I. Todo número negativo é irracional. (falso)
O número -2, por exemplo, é racional, uma vez que \(-2=\frac{-2}{1}\).
II. \(Z\subset I\) (falso)
Todo número inteiro pode ser escrito como uma fração com denominador 1. Por exemplo, \(7=\frac{7}{1}\). Assim, Z⊄I.
III. \(\sqrt4\) é um número racional. (verdadeiro)
\(\sqrt4=2\), que é racional.