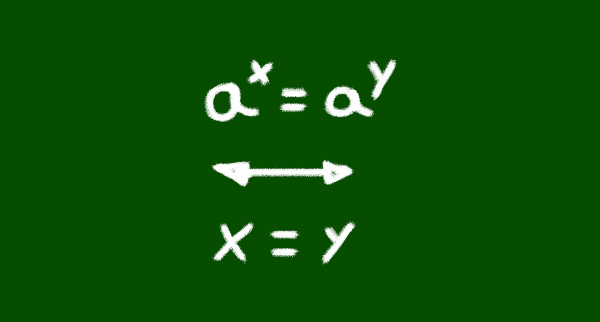Uma equação logarítmica apresenta a incógnita na base do logaritmo ou no logaritmando. Lembrando que um logaritmo possui o seguinte formato:
loga b = x ↔ ax = b,
*a é a base do logaritmo, b é o logaritmando e x é o logaritmo.
Ao resolver equações logarítmicas, devemos ter ciência das propriedades operatórias dos logaritmos, pois elas podem facilitar o desenvolvimento dos cálculos. Há, até mesmo, algumas situações em que não é possível resolver a equação sem lançar mão dessas propriedades.
Para resolver equações logarítmicas, aplicamos os conceitos tradicionais de resolução de equações e de logaritmos até que a equação chegue a dois possíveis casos:
1º) Igualdade entre logaritmos de mesma base:
Se ao resolver uma equação logarítmica, chegarmos a uma situação de igualdade entre logaritmos de mesma base, basta igualar aos logaritmandos. Exemplo:
loga b = loga c → b = c
2º) Igualdade entre um logaritmo e um número real
Se a resolução de uma equação logarítmica resultar na igualdade de um logaritmo e um número real, basta aplicar a propriedade básica do logaritmo:
loga b = x ↔ ax = b
Veja alguns exemplos de equações logarítmicas:
1° Exemplo:
log2 (x + 1) = 2
Vamos testar a condição de existência desse logaritmo. Para tanto, o logaritmando deve ser maior do que zero:
x + 1 > 0
x > – 1
Nesse caso, temos um exemplo do 2º caso, portanto, desenvolveremos o logaritmo da seguinte forma:
log2 (x + 1) = 2
22 = x + 1
x = 4 – 1
x = 3
2° Exemplo:
log5 (2x + 3) = log5 x
Testando as condições de existência, temos:
| 2x + 3 > 0 2x > – 3 x > – 3/2 |
x > 0 |
Nessa equação logarítmica, há um exemplo do 1º caso. Como há uma igualdade entre logaritmos de mesma base, devemos formar uma equação apenas com os logaritmandos:
log5 (2x + 3) = log5 x
2x + 3 = x
2x – x = – 3
x = – 3
3° Exemplo:
log3 (x + 2) – log3 (2x) = log3 5
Verificando as condições de existência, temos:
| x + 2 > 0 x > – 2 |
2x > 0 x > 0 |
Aplicando as propriedades do logaritmo, podemos escrever a subtração de logaritmos de mesma base como um quociente:
log3 (x + 2) – log3 (2x) = log3 5
log3 (x + 2) – log3 (2x) = log3 5
![]()
Chegamos a um exemplo do 1º caso, portanto devemos igualar os logaritmandos:
x + 2 = 5
2x
x + 2 = 10x
9x = 2
x = 2/9
4° exemplo:
logx – 1 (3x + 1) = 2
Ao verificar as condições de existência, devemos analisar também a base do logaritmo:
| x – 1 > 0 x > 1 |
3x + 1 > 0 3x > – 1 x > – 1/3 |
Essa equação logarítmica pertence ao 2° caso. Resolvendo-a, temos:
logx – 1 (3x + 1) = 2
(x – 1)2 = 3x + 1
x² – 2x + 1 = 3x + 1
x² – 5x = 0
x.(x – 5) = 0
x' = 0
x'' – 5 = 0
x'' = 5
Observe que pelas condições de existência (x > 1), a solução x' = 0 não é possível. Portanto, a única solução para essa equação logarítmica é x'' = 5.
5° exemplo:
log3 log6 x = 0
Aplicando as condições de existência, temos que x > 0 e log6 x> 0. Logo:
log3 (log6 x) = 0
30 = log6 x
log6 x = 1
61 = x
x = 6