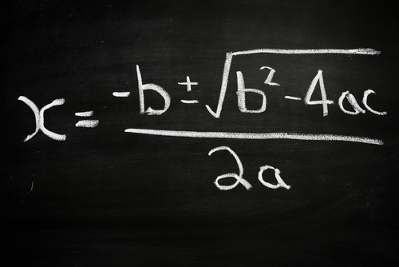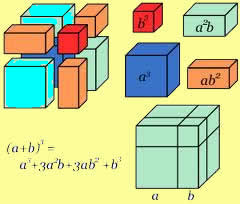As equações irracionais são assim classificadas quando ao menos uma incógnita da equação encontra-se em um radicando. Através dos exemplos a seguir, desenvolveremos estratégias para resolvê-las.
1° Tipo
Entre as equações irracionais, essa é a forma ideal. Para resolvê-la, o radical deve ser eliminado. Para isso, basta elevar ao quadrado ambos os membros da equação.
.jpg)
2x2 + 3x – 1 = (x + 1)2
Relembrando os conceitos de “Produtos Notáveis”, há no segundo membro da equação um caso de “quadrado da soma”. Vamos desenvolvê-lo e, em seguida, organizar os termos da equação a fim de escrevê-la como uma tradicional equação do 2° grau.
2x2 + 3x – 1 = x2 + 2x + 1
2x2 – x2 + 3x – 2x – 1 – 1 = 0
x2 + x – 2 = 0
Agora aplicamos a Fórmula de Bhaskara:
∆ = b2 – 4.a.c
∆ = (1)2 – 4.1.(- 2)
∆ = 1 + 8
∆ = 9
Portanto:
x = – b ± √∆
2.a
x = – 1 ± √9
2
x = – 1 ± 3
2
x' = – 1 + 3 = 2 = 1
2 2
x' = – 1 – 3 = – 4 = – 2
2 2
As raízes dessa equação são 1 e – 2.
2° Tipo
.jpg)
Para resolver essa equação, inicialmente procedemos como no caso anterior, ou seja, elevamos ao quadrado ambos os membros da equação.
.jpg)
O termo “–1” passará para o segundo membro da equação e, assim, teremos formada uma equação do 1° tipo. Assim, ela poderá ser resolvida analogamente à anterior.
.jpg)
x4 + 3x2 – 3x + 1 = (x2 + 1)2
Há novamente um caso de produtos notáveis. Basta desenvolver o quadrado da soma no segundo membro da equação.
x4 + 3x2 – 3x + 1 = x4 + 2x2 + 1
x4 – x4 + 3x2 – 2x2 – 3x + 1 – 1 = 0
x2 – 3x = 0
Podemos resolver essa equação do 2° grau colocando o x como fator em evidência:
x(x – 3) = 0
x' = 0
x'' – 3 = 0 → x'' = 3
As raízes dessa equação são 0 e 3.
3° Tipo
.jpg)
Novamente, vamos elevar ao quadrado ambos os lados da equação:
4. (4x2 – 8x – 5) = 4x2 – 16x – 20
4x2 – 8x – 5 = 4x2 – 16x – 20
4
4x2 – 8x – 5 = x2 – 4x – 5
4x2 – x2 – 8x + 4x – 5 + 5 = 0
3x2 – 4x = 0
x(3x – 4) = 0
x' = 0
3x'' – 4 = 0 → x'' = 4
3
As raízes dessa equação são 0 e 4/3
Essas são as formas mais comuns com que as equações irracionais costumam apresentar-se. Em geral, nós devemos sempre isolar a raiz em um membro da equação para que, ao elevar ambos os lados da equação à potência cujo expoente seja igual ao índice da raiz, consigamos eliminar a raiz e possamos resolver a equação da forma em que ela apresentar-se.