Equações trigonométricas são igualdades que possuem, pelo menos, uma razão trigonométrica na qual a incógnita é um ângulo desconhecido. Geralmente, nas equações trigonométricas, esse ângulo é convertido para um arco correspondente, e sua medida é dada em radianos.
Assim, são exemplos de equações trigonométricas:
senx = ½
cosx = √3/2
1 – sen2x = 1 + sen2x
As equações trigonométricas podem ser reduzidas a uma das três equações a seguir:
senx = senα
cosx = cosα
tgx = tgα
Para que as equações trigonométricas sejam assim reduzidas, é necessário usar as relações fundamentais da Trigonometria. Essas três equações são chamadas equações fundamentais da Trigonometria ou apenas equações trigonométricas.
Fórmulas de solução das equações fundamentais
As equações fundamentais podem ser solucionadas por meio de fórmulas, que são obtidas fazendo uso do ciclo trigonométrico. Essas fórmulas são:
1) senx = senα:
senx = senα
x = α +2kπ ou x = π – α + 2kπ
2) cosx = cosα:
cosx = cosα
x = α +2kπ ou x = – α + 2kπ
x = ± α + 2kπ
A segunda parte dessa solução percorre o ciclo trigonométrico em seu sentido anti-horário. A solução em que ambas as partes percorrem o sentido horário e que também pode ser dada como solução da equação cosx = cosα é:
cosx = cosα
x = α +2kπ ou x = 2π – α + 2kπ
3) tgx = tgα
tgx = tgα
x = α +2kπ ou x = π + α + 2kπ
x = α + kπ
Exemplo
Determine o valor de x na equação senx = √3/2.
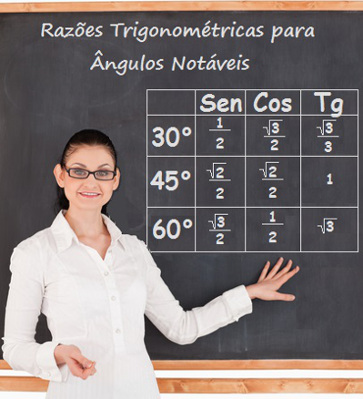
Observe que √3/2 = sen60°. Substituindo isso na fórmula de solução da equação senx, temos:
senx = sen60°
x = 60° +2kπ ou x = π – 60° + 2kπ
Entretanto, 60° não pode ser usado como solução de uma equação trigonométrica, pois não está expresso em radiano. Sabendo que π radianos é equivalente à meia volta – conhecimento adquirido a partir do ciclo trigonométrico – e que meia volta é equivalente a 180°, basta fazer a regra de três para descobrir a medida de 60° em radianos.
180° = π
60° x
180x = 60π
x = 60π
180
x = π
3
Então, a solução da equação é:
x = π +2kπ ou x = π – π/3 + 2kπ
x = π +2kπ ou x = 2π/3 + 2kπ
Informações importantes
Em qualquer das soluções das equações trigonométricas, ocorre a existência da parcela 2kπ. Essa parcela representa a quantidade de voltas que é dada no ciclo trigonométrico a fim de encontrar a solução das equações trigonométricas fundamentais.
Na solução da equação seno, suponha que essa equação seja definida apenas para a primeira volta, ou seja, apenas no intervalo que vai de 0°a 360°, ou de 0 a 2π. A solução dessa equação será:
senx = senα
x = α ou x = π – α
Considere agora que a mesma equação é válida também na segunda volta, ou seja, no intervalo que vai de 0 a 4π. Assim, a solução dessa equação será:
senx = senα
x = α +2π ou x = π – α + 2π
Imagine que a solução é válida para k + 1 voltas no ciclo trigonométrico, ou seja, no intervalo que vai de 0 a 2(k + 1)π. Então, a solução da equação seno será:
senx = senα
x = α +2kπ ou x = π – α + 2kπ
Essa ideia de voltas é idêntica para a equação cosseno. Já na equação tangente, uma ideia análoga é aplicada, mas no intervalo ]– π/2, π/2[.