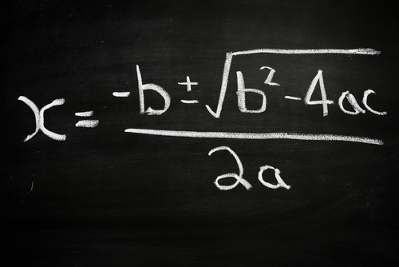Sempre que estamos resolvendo uma equação do 2° grau, é possível que esta possua duas raízes, uma raiz ou não possua raízes reais. Resolvendo uma equação da forma ax2 + bx + c = 0, utilizando a Fórmula de Bhaskara, podemos visualizar as situações em que cada uma ocorre. A fórmula de Bhaskara é definida por:
x = – b ± √? , onde ? = b2 – 4.a.c
2.a
Então, se ? < 0, isto é, se ? for um número negativo, será impossível encontrar √?. Dizemos então que, se ? > 0, logo a equação não possui raízes reais.
Caso tenhamos ? = 0, isto é, se ? for nulo, então √? = 0. Dizemos então que, se ? = 0, a equação possui apenas uma raiz real ou ainda podemos dizer que possui duas raízes idênticas.
Caso tenhamos ? > 0, isto é, se ? for um número positivo, então √? terá um valor real. Dizemos então que, se ? > 0, logo a equação possui duas raízes reais distintas.
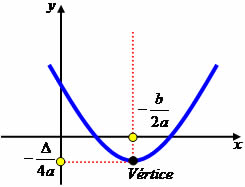
Vale lembrar que em uma função do 2° grau, o gráfico terá o formato de uma parábola. Essa parábola terá concavidade para cima (U) se o coeficiente a que acompanha o x2 for positivo. Mas terá concavidade para baixo (∩) se esse coeficiente for negativo.
Tome uma função do 2° grau qualquer do tipo f(x) = ax2 + bx + c. Vejamos como essas relações podem interferir no sinal de uma função do 2° grau.
1°) ? < 0
Caso o ? da função do 2° grau resulte em um valor negativo, não há um valor de x, tal que f(x) = 0. Portanto, a parábola não toca o eixo x.
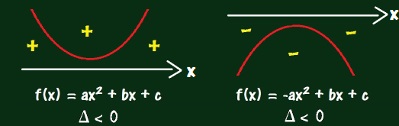
Quando o delta for negativo, a parábola não tocará o eixo x
2°) ? = 0
Caso o ? da função do 2° grau resulte em zero, então há apenas um valor de x, tal que f(x) = 0. Portanto, a parábola toca o eixo x em um único ponto.
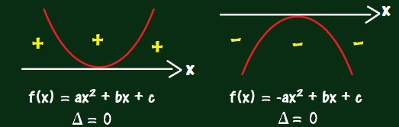
Quando o delta for zero, a parábola tocará o eixo x em um único ponto
3°) ? > 0
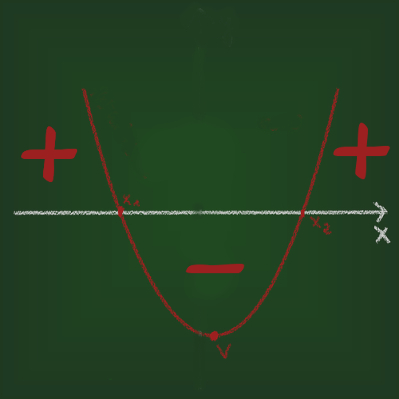
Caso o ? da função do 2° grau resulte em um valor positivo, então há dois valores de x, tal que f(x) = 0. Portanto, a parábola toca o eixo x em dois pontos.
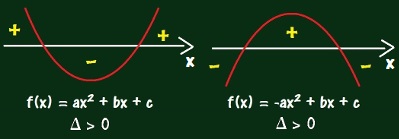
Quando o delta for positivo, a parábola tocará o eixo x em dois pontos
Vejamos alguns exemplos em que deveremos determinar o sinal de uma função do 2° grau em cada item:
|
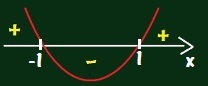
1) f(x) = x2 – 1 ? = b2 – 4 . a . c |
|
|
Essa é uma parábola com concavidade para cima e f(x) > 0 para x < – 1 ou x > 1 |
|
|
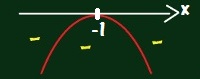
2) f(x) = – x2 + 2x – 1 ? = b2 – 4 . a . c |
|
|
Essa é uma parábola com concavidade para baixo e f(x) = 0 para x = – 1 |
|
3) f(x) = x2 – 2x + 3 ? = b2 – 4 . a . c |
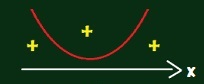 A parábola não toca o eixo x |
|
Essa é uma parábola com concavidade para cima e f(x) > 0 para todo x real |