Para compreender melhor os passos e a discussão feita neste artigo é necessário compreender a definição de função e os elementos que constituem uma função: Domínio, Contradomínio, Imagem . Para isso, façamos uma breve revisão quanto à definição e notação de uma função.
“Função é uma regra que nos diz como associar elementos de um conjunto (Conjunto A) a elementos de outro conjunto (Conjunto B). Portanto, dizemos que f é uma função caso ela associe todos os elementos (x de A) a elementos distintos do conjunto B”.
Notação:
![]()
Lê-se: f é uma função de A em B.
.png)
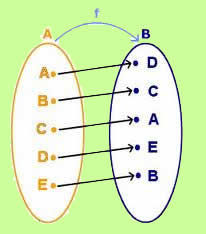
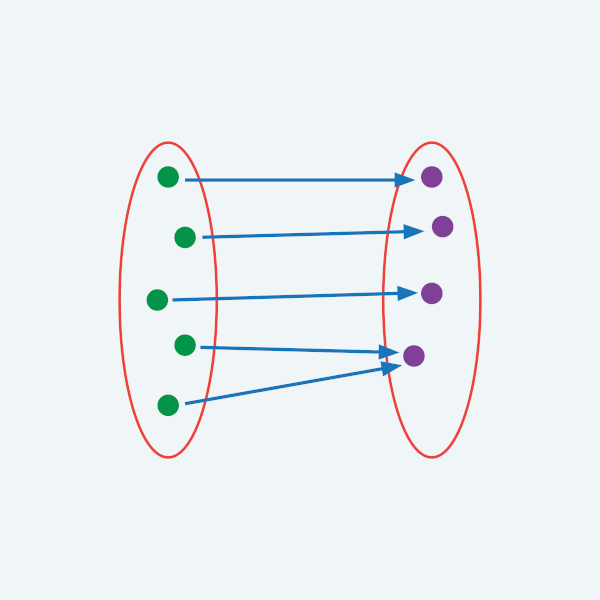
Acima temos a representação da função em um diagrama, que nos mostra elementos do domínio, contradomínio e imagem. A partir do momento em que condições são estabelecidas sobre esses elementos, começamos a obter propriedades que constituem novas concepções sobre as funções.
Uma dessas concepções é a da função injetora, que impõe a seguinte condição: elementos distintos de A são levados pela função em elementos distintos de B. Desse modo, pode-se afirmar que nenhum elemento de B será imagem para dois elementos de A. Vejamos a representação de algumas funções e analisemos se elas são de fato injetoras ou não:
.png)
Vimos duas representações, note que a primeira é uma função injetora, pois nenhum elemento do conjunto B (Contradomínio) é imagem de mais de um elemento do conjunto A (Domínio).
Em contrapartida, na segunda representação nota-se um elemento do conjunto B sendo imagem para dois elementos do conjunto A, contrariando a condição que define a função injetora.
Sendo assim, façamos uma definição de uma função injetora utilizando a linguagem matemática:
.png)
Analisemos uma função de forma algébrica utilizando a definição de função injetora.
Verifique se a função f(x) = x2 + 5 é injetora.
Para que ela seja injetora não podemos ter diferentes valores de x sendo elevados a valores iguais. O que acontece com números negativos elevados a potências pares? O resultado será positivo, portanto espera-se que ela não seja injetora, pois (2)2 = (-2)2.
Com dois números opostos, por exemplo -3 e 3, calcularemos sua imagem pela função dada.
![]()
Essa não é uma função injetora, pois temos a seguinte situação:
![]()
Aproveite para conferir nossa videoaula relacionada ao assunto: