A função sobrejetora é um caso particular de função. Função é uma relação entre dois conjuntos, A e B, sendo que para todo elemento do conjunto A existe um único correspondente no conjunto B. O conjunto A é conhecido como domínio, e o conjunto B é conhecido como contradomínio. A função sobrejetora, também conhecida como função sobrejetiva, é aquela em que todos os elementos do contradomínio são imagem de pelo menos um elemento do domínio. Sendo assim, o contradomínio é igual à imagem da função. Além de sobrejetora, uma função pode ser injetora ou bijetora.
Leia também: Função linear — um caso particular de função do 1º grau
Tópicos deste artigo
- 1 - O que é uma função sobrejetora?
- 2 - Exemplos de função sobrejetora
- 3 - Exemplos de função não sobrejetora
- 4 - Gráfico da função sobrejetora
- 5 - Gráfico de uma função não sobrejetora
- 6 - Função bijetora e função injetora
- 7 - Exercícios resolvidos sobre função sobrejetora
O que é uma função sobrejetora?
No estudo das funções, existem algumas classificações possíveis para a função, dependendo das suas características. Uma delas é a de função sobrejetora ou função sobrejetiva. Uma função é conhecida como sobrejetora quando o conjunto imagem da função é igual ao contradomínio da função. Assim, para que uma função seja sobrejetora é necessário que todos os elementos do contradomínio sejam correspondentes de pelo menos um elemento no domínio.
→ Definição formal
Dizemos que a função f : A → B é uma função sobrejetora se e somente se:
\(\forall\ b\ \epsilon\ B,\ \exists\ a\ \epsilon\ A\ |\ f(a)=b\)
Exemplos de função sobrejetora
-
Exemplo 1:
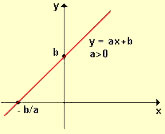
A função polinomial do primeiro grau, conhecida também como função afim, com domínio e contradomínio nos números reais, é uma função sobrejetora. Por exemplo, considere a função \(f:\ \mathbb{R}\ \rightarrow\mathbb{R}\) com lei de formação \(f\left(x\right)=x+1\).
Essa função é sobrejetora, pois no conjunto dos números reais, para todo valor real, y, existe um número real tal que x + 1 = y. Logo, o contradomínio é igual ao conjunto imagem, ou seja, todo elemento do domínio é imagem de algum elemento do contradomínio.
-
Exemplo 2:
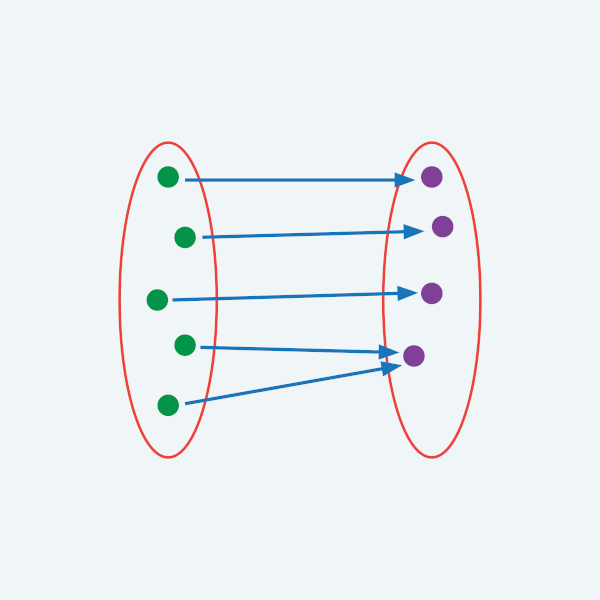
A função \(f:\ A\ \rightarrow B\), representada no diagrama a seguir, é uma função sobrejetora:
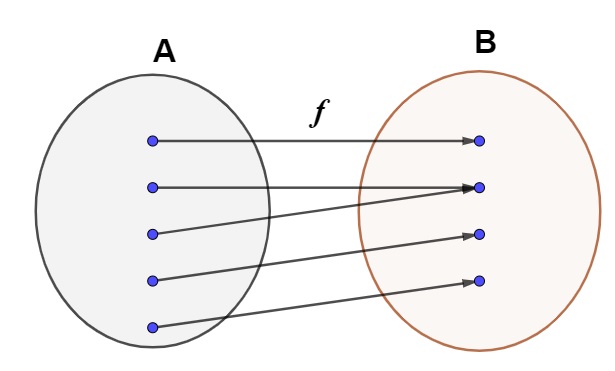
Note que todos os elementos do contradomínio são correspondentes de pelo menos um elemento do domínio, fazendo com que essa função seja sobrejetora.
Exemplos de função não sobrejetora
Agora veremos alguns casos de função que não são sobrejetoras.
-
Exemplo 1:
Vamos começar pela função \(f:\mathbb{R}\rightarrow\mathbb{R}\) com lei de formação \(f\left(x\right)=x^2\). Ela é conhecida como função do 2º grau ou função quadrática e não pode ser classificada como sobrejetora, pois sabemos que todo número ao quadrado gera um resultado positivo. Se nosso contradomínio é o conjunto dos números reais, os números negativos não são correspondentes de nenhum número no domínio, logo essa função não é sobrejetora.
Observação: É importante analisarmos o domínio e o contradomínio da função, e não só a sua lei de formação, pois se mudarmos o domínio ou o contradomínio da função, pode ser que ela deixe de ser sobrejetora ou que ela se torne sobrejetora. No exemplo anterior, se o domínio fosse os números reais positivos e o contradomínio também, com a mesma lei de formação, ou seja f(x) = x², essa função seria sobrejetora.
-
Exemplo 2:
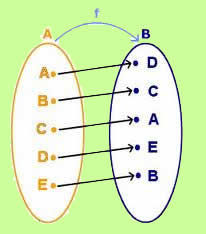
No diagrama a seguir, há a representação de uma função que não é sobrejetora:
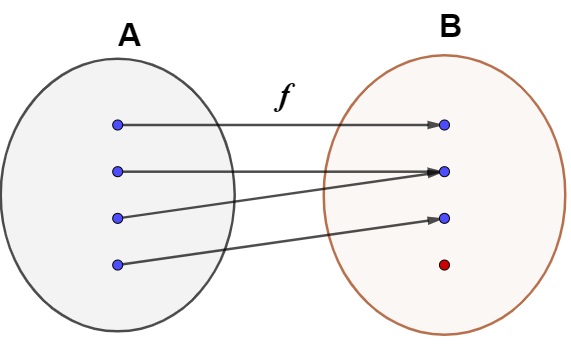
Note que no contradomínio, ou seja, no conjunto B, há um elemento que não é correspondente de nenhum elemento no conjunto A. Sendo assim, essa função não é sobrejetora.
Gráfico da função sobrejetora
Podemos analisar graficamente se a função é sobrejetora ou não. Uma função é sobrejetora se todos os valores do eixo y forem correspondentes de pelo menos um valor no eixo x.
-
Exemplo 1:
A seguir, representaremos o gráfico da função f(x) = x³:
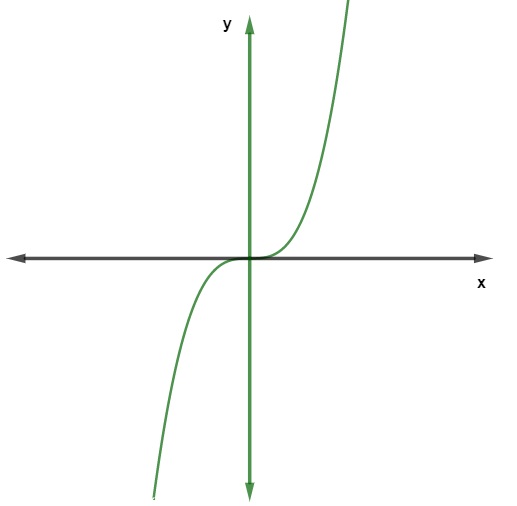
Note que todos os elementos de y são correspondentes de pelo menos um elemento de x, logo podemos concluir que nesse intervalo a função é sobrejetora.
Gráfico de uma função não sobrejetora
Agora, vejamos a representação gráfica da função f(x) = sen(x):
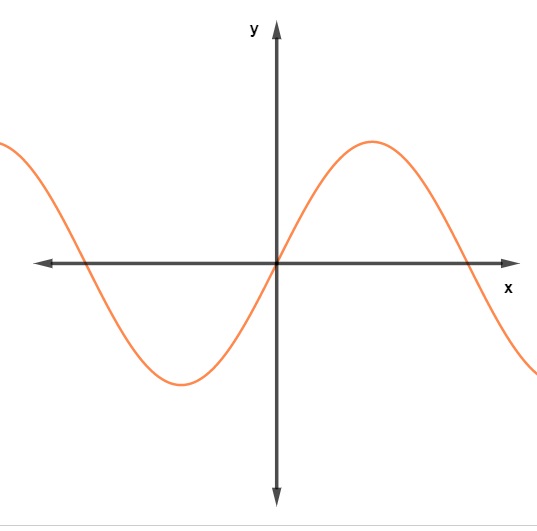
Note que, para esse intervalo, nem todos os valores de y são correspondentes de um valor do domínio. Sendo assim, para esse intervalo, podemos afirmar que essa função não é sobrejetora.
Saiba mais: Como construir o gráfico de uma função?
Função bijetora e função injetora
Além da função sobrejetora, existe a função injetora e a função bijetora.
-
Função injetora: uma função é conhecida como injetora quando existir um único correspondente de todo elemento do domínio no contradomínio.
-
Função bijetora: uma função é conhecida como bijetora se ela for injetora e sobrejetora ao mesmo tempo.
Exercícios resolvidos sobre função sobrejetora
Questão 1
Sobre a definição de função sobrejetora, marque a alternativa correta:
A) Toda função é sobrejetora.
B) Uma função é sobrejetora se todo elemento do domínio possuir um correspondente no contradomínio.
C) Uma função é sobrejetora se todo elemento do contradomínio for correspondente de pelo menos um elemento no domínio.
D) Uma função é sobrejetora se todo elemento do contradomínio for correspondente de um único elemento do domínio.
E) Uma função é sobrejetora quando o contradomínio e o domínio são iguais.
Resolução:
Alternativa C
Para que a função seja sobrejetora, é necessário que todo elemento do contradomínio seja correspondente de pelo menos um elemento do domínio.
Questão 2
Analise a representação gráfica a seguir:
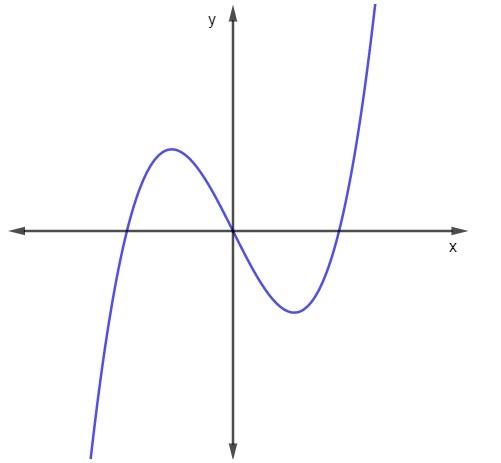
Sobre o gráfico da função para esse intervalo, podemos afirmar que:
A) essa função é linear.
B) essa função é injetora.
C) essa função é composta.
D) essa função é sobrejetora.
E) essa função é quadrática.
Resolução:
Alternativa D
Podemos perceber que todos os elementos do contradomínio, ou seja, do eixo y, são correspondentes de pelo menos um elemento do domínio, ou seja, do eixo x. Sendo assim, esse gráfico esboça uma função sobrejetora.