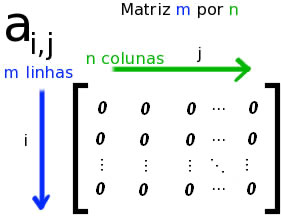
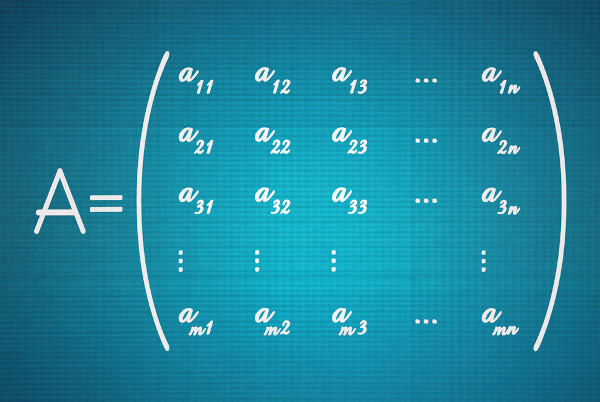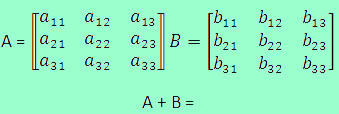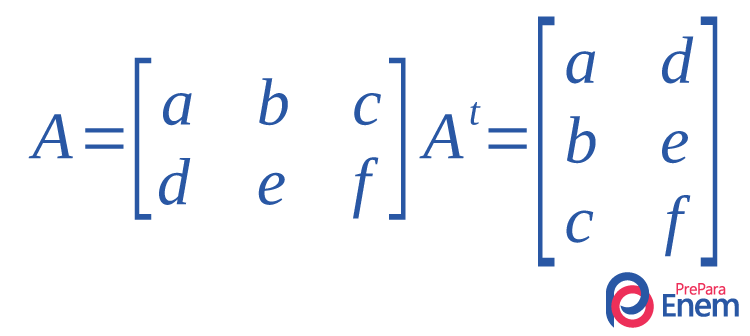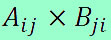A matriz é uma representação em tabela de um conjunto de elementos. De forma geral, dizemos que uma matriz é formada por m linhas e n colunas. Cada elemento da matriz — também chamado de entrada da matriz — se localiza no cruzamento entre uma linha e uma coluna. Para indicar essa posição, representamos o elemento por uma letra minúscula acompanhada de dois subíndices numéricos: o primeiro informando a linha, e o segundo, a coluna. Assim, por exemplo, o elemento que ocupa a posição na primeira linha e segunda coluna de uma matriz A é escrito como \(a_{12}\).
Leia também: Menor complementar — um número associado a cada um dos elementos da matriz
Tópicos deste artigo
- 1 - Resumo sobre matriz
- 2 - Como é a representação de uma matriz?
- 3 - Quais são os elementos de uma matriz?
- 4 - Quais são os tipos de matrizes?
- 5 - Operações com matrizes
- 6 - Diferenças entre matriz e determinante
- 7 - Exercícios resolvidos sobre matriz
Resumo sobre matriz
-
Matriz é uma representação em tabela em que as disposições horizontais são chamadas de linhas e as verticais, de colunas.
-
Uma matriz A com m linhas e n colunas é indicada por \(A_{mxn}\).
-
O elemento de uma matriz A que ocupa a posição no cruzamento entre a linha i e a coluna j é indicado por \(a_{ij}\).
-
Os tipos mais comuns de matrizes são a linha, coluna, nula, quadrada, identidade, transposta, simétrica e inversa.
-
As principais operações com matriz são a adição, a subtração, a multiplicação por um número e a multiplicação entre matrizes.
-
O determinante é um número associado a uma matriz quadrada por uma relação matemática.
Como é a representação de uma matriz?
Uma matriz é escrita por uma letra maiúscula com subíndices que indicam a quantidade de linhas e a quantidade de colunas, respectivamente. Assim, uma matriz A com m linhas e n colunas é escrita como \(A_{mxn}\), e mxn (lê-se “m por n”) é chamado de ordem da matriz A. Para representar uma matriz, exibimos seus elementos entre colchetes ou chaves. Veja o exemplo:
\(A =\begin{bmatrix} 3 & 9 & -7 \\ 0 & -12 & 1\end{bmatrix}\) ou \(A =\begin{pmatrix} 3 & 9 & -7 \\ 0 & -12 & 1\end{pmatrix}\)
Nesse exemplo, a matriz A possui duas linhas e três colunas. Escrevemos \(A_{2x3}\). A primeira linha é formada pelos elementos 3, 9 e -7, e a segunda, pelos elementos 0, -12 e 1. A primeira coluna é formada pelos elementos 3 e 0; a segunda coluna, pelos elementos 9 e -12; e a terceira, pelos elementos -7 e 1.
Quais são os elementos de uma matriz?
Os elementos de uma matriz, em geral, são números ou letras. Cada elemento possui uma posição específica no cruzamento de determinada linha e determinada coluna.
Para representar essa localização, indicamos o elemento por uma letra minúscula com dois subíndices numéricos, o primeiro informando a linha, e o segundo, a coluna. Veja o exemplo a seguir:
\(A =\begin{bmatrix} 3 & 9 & -7 \\ 0 & -12 & 1\end{bmatrix}\)
O elemento 3 ocupa a posição no cruzamento da primeira linha com a primeira coluna. Portanto, \(a_{11}=3\). O elemento 9 ocupa a posição no cruzamento da primeira linha com a segunda coluna. Portanto, \(a_{12}=9\). O elemento -7 ocupa a posição no cruzamento da primeira linha com a terceira coluna. Portanto, \(a_{13}=-7\).
Além disso, o elemento 0 ocupa a posição no cruzamento da segunda linha com a primeira coluna. Portanto, \(a_{21}=0\). O elemento -12 ocupa a posição no cruzamento da segunda linha com a segunda coluna. Portanto, \(a_{22}=-12\). O elemento 1 ocupa a posição no cruzamento da segunda linha com a terceira coluna. Portanto, \(a_{23}=1\).
De modo geral, podemos representar por \(a_{ij}\) o elemento que ocupa a posição do cruzamento da linha i com a coluna j. Assim, a representação da forma geral de uma matriz A com m linhas e n colunas é a seguinte:
\(\begin{bmatrix} a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\ a_{21} & a_{22} & a_{23} & \cdots & a_{2n} \\ a_{31} & a_{32} & a_{33} & \cdots & a_{3n} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & a_{m3} & \cdots &a_{mn} \\ \end{bmatrix}\)
Quais são os tipos de matrizes?
Os principais tipos de matrizes são a matriz linha, coluna, nula, quadrada, identidade, transposta e simétrica. Vejamos a seguir o que caracteriza cada um.
→ Matriz linha
Matriz linha é uma matriz que possui apenas uma linha. Veja o exemplo:
\(\begin{bmatrix} 4 & 6 & -10 & 3\end{bmatrix}\)
→ Matriz coluna
Matriz coluna é uma matriz que possui apenas uma coluna. Veja o exemplo:
\(\begin{bmatrix} -1 \\ 9 \\ 82\end{bmatrix}\)
→ Matriz nula
Matriz nula é uma matriz em que todos os elementos são zero. Veja o exemplo:
\(\begin{bmatrix} 0 & 0 & 0 \\ 0 & 0 & 0\end{bmatrix}\)
→ Matriz quadrada
Matriz quadrada é uma matriz em que o número de linhas é igual ao número de colunas. Dada uma matriz quadrada \(A_{nxn}\), dizemos que a ordem de A é n. Veja os exemplos:
\(\begin{bmatrix} 5 & 17 \\ -7 & 84\end{bmatrix}\)
\(\begin{bmatrix} -4 & 1 & 0 \\ 31 & 64 & 102 \\ 0 & -1 & 15\end{bmatrix}\)
Importante: Chamamos de diagonal principal os elementos \(a_{ij}\) de uma matriz quadrada que satisfazem \(i=j\) e de diagonal secundária os elementos \(a_{ij}\) que satisfazem \(i+j = n+1\), em que n é a ordem da matriz quadrada. Veja o exemplo:
\(B=\begin{bmatrix} -11 & 6 \\ 8 & 0\end{bmatrix}\)
B é uma matriz de ordem 2. A diagonal principal da matriz B é formada pelos elementos -11 e 0 (que são indicados, respectivamente, por \(a_{11}\) e \(a_{22}\)). A diagonal secundária da matriz B é formada pelos elementos 6 e 8 (que são indicados, respectivamente, por \(a_{12}\) e \(a_{21}\)).
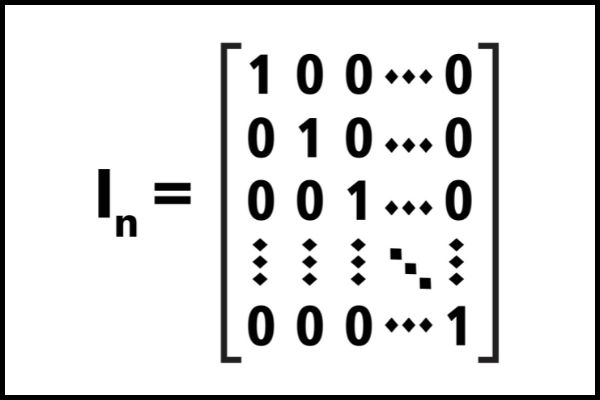
→ Matriz identidade
Matriz identidade é uma matriz quadrada em que os elementos da diagonal principal são 1 e os demais elementos são 0. A matriz identidade de ordem n é representada por \(I_n\). Veja o exemplo:
\(I_3=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\)
→ Matriz transposta
Matriz transposta é uma matriz com as linhas trocadas por colunas (e vice-versa) em relação a outra matriz. Em outras palavras, se A é uma matriz com elementos \(a_{ij}\), sua transposta é uma matriz com os elementos \(a_{ij}\). A matriz transposta de A é representada por \(A^t\). Veja o exemplo:
Considere a seguinte matriz A.
\(A=\begin{bmatrix} 13 & 4 & 15 \\ -8 & 2 & 1 \\ 0 & -5 & 77\end{bmatrix}\)
A matriz transposta de A é
\(A^t=\begin{bmatrix} 13 & -8 & 0 \\ 4 & 2 & -5 \\ 15 & 1 & 77\end{bmatrix}\)
→ Matriz simétrica
Matriz simétrica é uma matriz em que \(a_{ij}=a_{ji}\) para todo i e j. Ou seja, é uma matriz que é igual à sua transposta. Veja o exemplo:
\(B=\begin{bmatrix} -1 & 5 \\ 5 & 0\end{bmatrix}\)
\(B^t=\begin{bmatrix} -1 & 5 \\ 5 & 0\end{bmatrix}\)
Veja também: Matriz triangular — a matriz quadrada em que os elementos acima ou abaixo da diagonal principal são nulos
Operações com matrizes
→ Adição e subtração de matrizes
Para adicionar ou subtrair duas matrizes, devemos operar os elementos nas posições correspondentes. Assim, as matrizes envolvidas devem possuir a mesma ordem, que também será a ordem da matriz resultante.
-
Exemplo 1:
Considerando as matrizes A e B abaixo, quanto é \(A + B\)?
\(A=\begin{bmatrix} 0 & 2 \\ 6 & -4\end{bmatrix}\)
\(B=\begin{bmatrix} -2 & 25 \\ 10 & 8\end{bmatrix}\)
Resolução:
\(A+B=\begin{bmatrix} 0+(-2) & 2+25 \\ 6+10 & -4+8\end{bmatrix} =\begin{bmatrix} -2 & 27\\ 16 & 4\end{bmatrix}\)
-
Exemplo 2:
Considerando as matrizes A e B abaixo, quanto é \(A - B\)?
\(A=\begin{bmatrix} 0 & 2 \\ 6 & -4\end{bmatrix}\)
\(B=\begin{bmatrix} -2 & 25 \\ 10 & 8\end{bmatrix}\)
Resolução:
\(A-B=\begin{bmatrix} 0-(-2) & 2-25 \\ 6-10 & -4-8\end{bmatrix} =\begin{bmatrix} 2 & -23\\ -4 & -12\end{bmatrix}\)
→ Multiplicação de matriz por um número
Para multiplicar uma matriz por um número, devemos multiplicar o número por cada elemento da matriz.
-
Exemplo:
Considere a matriz A abaixo.
\(A=\begin{bmatrix} 1 & 2 & 3 \\ -3 & 7 & 0 \\ 8& -5 & 4\end{bmatrix}\)
A matriz 2A é
\(2A=\begin{bmatrix} 2\cdot1 & 2\cdot 2 & 2\cdot 3 \\ 2\cdot (-3) & 2\cdot 7 & 2\cdot 0 \\ 2\cdot 8 & 2\cdot (-5) & 2\cdot 4\end{bmatrix} =\begin{bmatrix} 2 & 4 & 6\\ -6 & 14 & 0 \\ 16 & -10 & 8\end{bmatrix}\)
Observe que as matrizes A e 2A possuem ordem 3.
→ Multiplicação de duas matrizes
A multiplicação de duas matrizes pode parecer difícil à primeira vista, pois utiliza um procedimento um pouco diferente, como veremos adiante. Antes, é importante destacar dois aspectos: nem sempre é possível multiplicar duas matrizes, e a multiplicação de matrizes não é comutativa (ou seja, A·B é diferente de B·A).
Para que a multiplicação aconteça, a quantidade de colunas da primeira matriz deve ser igual à quantidade de linhas da segunda matriz. Além disso, a matriz resultante terá a quantidade de linhas igual à da primeira matriz e a quantidade de colunas igual à da segunda matriz.
Considere que vamos multiplicar uma matriz A por uma matriz B. Para obter cada elemento da matriz resultante, devemos multiplicar os elementos da linha correspondente da matriz A pelos elementos da coluna correspondente da matriz B e somar os valores obtidos.
-
Exemplo:
Considerando as matrizes A e B abaixo, quanto é \(A ⋅B\)?
\(A=\begin{bmatrix} 3 & 11 & -6 \\ 4 & -2 &10 \\ \end{bmatrix}\)
\(B=\begin{bmatrix} -3 & 2 \\ 1& -8 \\ 0& 5\end{bmatrix}\)
Resolução:
Perceba que a multiplicação \(A ⋅B\) é possível, pois A possui 3 colunas e B possui 3 linhas. Além disso, a ordem de \(A ⋅B\) será 2x2, pois A possui 2 linhas e B possui 2 colunas. Assim,
\(A\cdot B=\begin{bmatrix} c_{11} & c_{12} \\ c_{21}& c_{22} \\ \end{bmatrix}\)
Obtemos os elementos de \(A ⋅B\) da seguinte forma:
\(c_{11}=3⋅(-3)+11⋅1+(-6)⋅0 = 2\)
\(c_{12}=3⋅2+11⋅(-8)+(-6)⋅5 = -112\)
\(c_{21}=4⋅(-3)+(-2)⋅1+10⋅0 = -14\)
\(c_{22}=4⋅2+(-2)⋅(-8)+10⋅5 = 74\)
Logo,
\(A\cdot B=\begin{bmatrix} 2 & -112 \\ -14& 74 \\ \end{bmatrix}\)
Importante: Se A e B são matrizes quadradas de ordem n, e uma matriz B é tal que \(A⋅B=I_n\), então B é chamada de matriz inversa de A e é representada por \(A^{-1}\).
Diferenças entre matriz e determinante
-
Matriz: é a representação em tabela de um conjunto de elementos, formada por m linhas e n colunas.
-
Determinante: é um número real associado especificamente a uma matriz quadrada e que possui várias aplicações, como na resolução de sistemas lineares e para verificar se três pontos são colineares.
Saiba mais: Quais são as propriedades dos determinantes?
Exercícios resolvidos sobre matriz
Questão 1
Se \(A=\begin{bmatrix} 1 &3 \\ 0&2 \\ \end{bmatrix}\) e \(B=\begin{bmatrix} 0 &1 \\ 4&-1 \\ \end{bmatrix}\), qual alternativa representa a matriz A + B?
A) \(\begin{bmatrix} 3 &1 \\ 1&-1 \\ \end{bmatrix}\)
B) \(\begin{bmatrix} 2 &3 \\ 3&-2 \\ \end{bmatrix}\)
C) \(\begin{bmatrix} 1 &4 \\ 4&1 \\ \end{bmatrix}\)
D) \(\begin{bmatrix} 0 &2 \\ 1&-2 \\ \end{bmatrix}\)
E) \(\begin{bmatrix} 1 &3 \\ 4&-2 \\ \end{bmatrix}\)
Resolução:
Alternativa C.
\(A+B=\begin{bmatrix} 0+1 & 3+1 \\ 0+4 & 2+(-1)\end{bmatrix} =\begin{bmatrix} 1 & 4\\ 4 & 1\end{bmatrix}\)
Questão 2
Considere \(\begin{bmatrix} 1 &2 & y \\ x&-5 & z \\ -2 & -1 & 7 \end{bmatrix}\). Se A é uma matriz simétrica, então os valores de x, y e z são, respectivamente, iguais a
A) 2, 0 e 1.
B) 3, 5 e -1.
C) -2, 0 e 3.
D) 2, -2 e -1.
E) 3, -5 e -3.
Resolução:
Alternativa D.
Se A é uma matriz simétrica, então \(a_{ij}=a_{ji}\) para todo i e j. Ou seja,
\(a_{21}=a_{12}\Rightarrow x=2\)
\(a_{13}=a_{31}\Rightarrow y=-2\)
\(a_{23}=a_{32}\Rightarrow z=-1\)