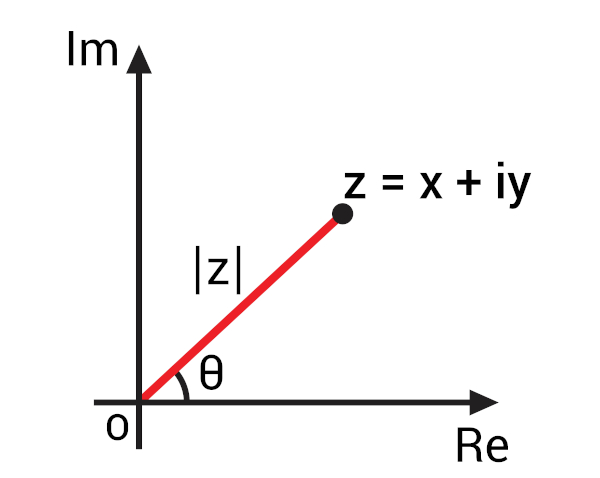
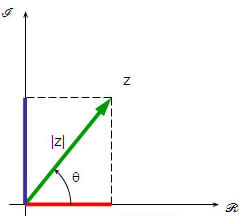
Sabemos que número complexo é um par ordenado de números reais z = (a, b). Todo número complexo do tipo z = (a, b) pode ser escrito na forma normal ou algébrica: z = a + bi. Representando esse número complexo no plano de Argand-Gauss e utilizando alguns recursos da trigonometria e o teorema de Pitágoras, podemos escrevê-lo na forma trigonométrica: z = |z|(cos θ + i.sen θ).
A forma trigonométrica é muito útil na realização das operações de multiplicação e divisão envolvendo números complexos, em razão da sua praticidade nos cálculos.
Multiplicação na forma trigonométrica.
Considere dois números complexos quaisquer, escritos na forma trigonométrica:
z1 = |z1 |∙(cosθ + i∙sen θ) e z2 = |z2 |(cos α+i∙sen α)
O produto entre z1 e z2 pode ser feito da seguinte forma:
z1 ∙ z2 = |z1 |∙|z2 |∙[cos(θ+α) +i∙sen (θ+α) ]
Tal fato é garantido pelas relações:
sen(θ + α) = senθ ∙ cosα + senα∙cosθ
cos(θ + α) = cosθ ∙ cosα - senθ∙senα
Exemplo 1: Dados os números complexos z1 = 6∙(cos30o + i∙sen 30o) e z2 = 3∙(cos15o + i∙sen 15o), calcule o valor de z1 ∙ z2.
Solução: Utilizando a fórmula da multiplicação de números complexos na forma trigonométrica, temos que:
z1 ∙ z2 = 6∙3∙[cos(30o + 15o )+i∙sen (30o + 15o )]
z1 ∙ z2 = 18∙(cos45o + i∙sen 45o )
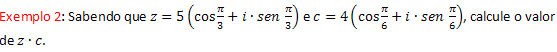
Solução: Utilizando a fórmula da multiplicação, obtemos:
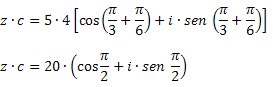
Divisão na forma trigonométrica
Para realizar a divisão na forma trigonométrica também existe uma fórmula que facilita os cálculos.
Sejam z1 = |z1 |∙(cosθ + i∙sen θ) e z2 = |z2 |(cosα + i∙senα), dois números complexos quaisquer, o quociente entre z1 e z2 será dado por:
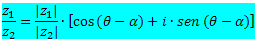
Exemplo 3: Dados z = 22∙(cos120o + i∙sen 120o) e c = 11∙(cos90o +i∙sen 90o), determine o valor de z/c.
Solução: Pela fórmula da divisão de complexos na forma trigonométrica, temos que: