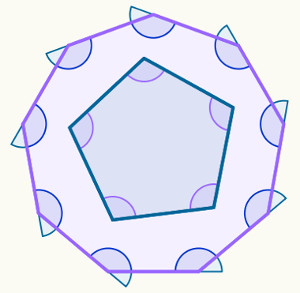
Um polígono é uma linha fechada formada apenas por segmentos de reta que não se cruzam e que estão em um mesmo plano. Dessa maneira, os polígonos são figuras geométricas formadas por lados, os quais são justamente os segmentos de reta dados na definição.
Um polígono é dito regular quando possui três características:
1 – é convexo;
2 – todos os seus lados possuem a mesma medida;
3 – todos os seus ângulos são congruentes.
Para compreender melhor essa definição e antes de apresentar os primeiros exemplos, vale relembrar o que são polígonos convexos, já que esse é um requisito para que sejam regulares.
Definição de polígono convexo
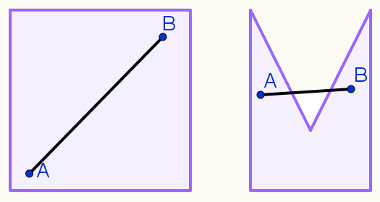
Um polígono é convexo quando, dados os pontos A e B quaisquer em seu interior, todos os pontos do segmento AB também estão no interior do polígono, independentemente da localização dos pontos AB.
Se, pelo menos um ponto do segmento AB estiver no exterior do polígono, ele é dito não convexo.
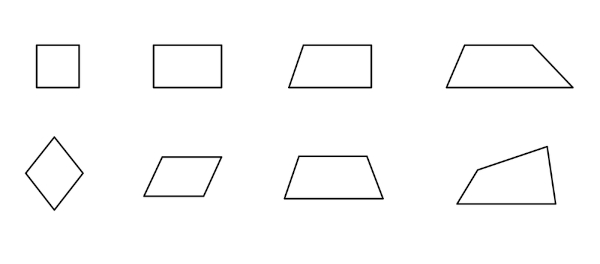
Na imagem acima, à esquerda, um exemplo de um polígono em que, independentemente da localização dos pontos A e B, todos os pontos do segmento AB sempre estarão em seu interior. Já à direita, um exemplo de polígono em que os dois pontos A e B estão em seu interior, mas uma parte do segmento AB está fora do polígono.
Um polígono também pode ser dito não convexo quando ele possui “reentrâncias”.
Exemplo de polígono regular
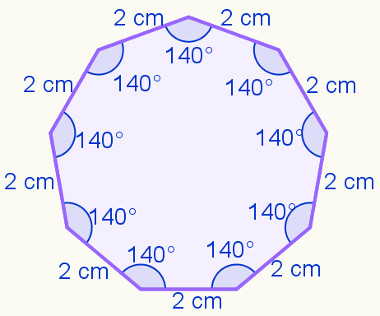
O polígono presente na imagem a seguir não possui reentrâncias, possui todos os lados com medidas iguais e tem todos os ângulos congruentes. Assim sendo, ele é um polígono regular.
Propriedades dos polígonos regulares
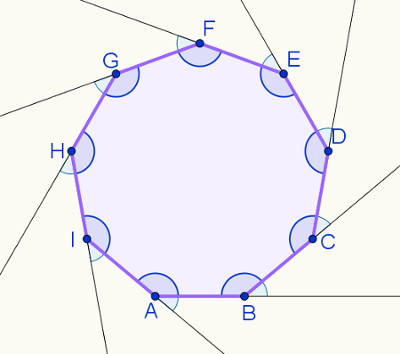
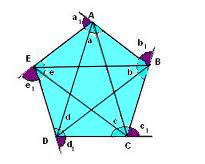
1ª – Todo polígono regular de n lados possui também n arestas, n ângulos internos, n vértices e n ângulos externos. A figura a seguir mostra um exemplo de polígono regular com todas essas medidas e elementos:
2ª – Somente dos polígonos regulares, ou daqueles em que existam mais hipóteses a considerar, será possível descobrir a medida de cada ângulo interno. No caso dos polígonos regulares, basta calcular a soma dos ângulos internos e depois dividir esse resultado pelo número de ângulos que foi somado. Evidentemente, esse número é igual ao número de lados do polígono.
Também podemos desenvolver uma fórmula para esse procedimento. Seja L a medida de um ângulo interno de um polígono regular, ele pode ser dado por:
L = (n – 2)180
n
Em que n é o número de lados do polígono.
Por exemplo, no eneágono, cada ângulo interno mede 140°, pois:
L = (n – 2)180
n
L = (9 – 2)180
9
L = (7)180
9
L = 1260
9
L = 140°
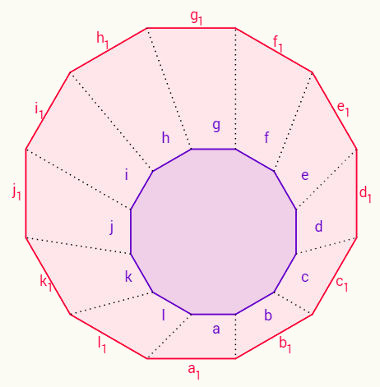
3ª – A medida de cada um dos ângulos externos de um polígono regular pode ser obtida dividindo a soma dos ângulos externos do polígono pelo número de ângulos externos que ele possui. Lembrando que a quantidade de ângulos externos é igual à quantidade de lados.
Em termos matemáticos, temos o seguinte, considerando que M seja cada ângulo externo:
M = 360
n
No eneágono, por exemplo, cada ângulo externo mede 40°, pois:
M = 360
n
M = 360
9
M = 40°