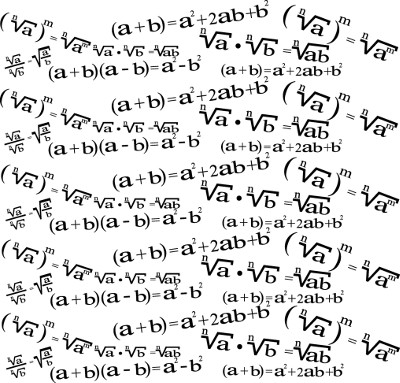Polinômios são expressões formadas pela adição algébrica de monômios. Estes, por sua vez, são compostos pelo produto entre números conhecidos (coeficientes) e números desconhecidos (incógnitas). Dessa maneira, os polinômios também podem ser definidos como expressões algébricas.
A seguir, confira um exemplo de polinômio que bate com a definição dada anteriormente.
4x2y + 9ka – 17 xy
Esse polinômio é chamado de trinômio porque possui três parcelas. Polinômios que possuem duas parcelas são chamados de binômios, e aqueles que possuem mais de três parcelas são conhecidos apenas como polinômios.
Grau de um polinômio
O grau do polinômio é igual ao maior grau entre todos os monômios que o formam. Por isso, é importante saber como encontrar o grau do monômio para conseguir encontrar o grau do polinômio.
O grau do monômio é dado pela quantidade de incógnitas que ele possui. Dessa maneira, o monômio 4x4y3, por exemplo, possui grau 7.
Adição e subtração de polinômios
A soma e a subtração de polinômios são feitas termo a termo e só é possível entre termos que possuem parte literal igual, isto é, os chamados termos semelhantes. Dessa maneira, aconselhamos que os termos semelhantes sejam colocados lado a lado, antes de mais nada, em uma adição ou subtração de polinômios.
Na realidade, após conhecer as operações entre números inteiros, os conceitos de soma e subtração misturam-se. Por isso, ao efetuar uma adição de polinômios, faremos jogo de sinais, adições e subtrações que forem necessários.
Multiplicação de polinômios
Quando multiplicamos um polinômio por um monômio, devemos multiplicar cada termo desse polinômio por esse monômio.
Multiplique coeficiente por coeficiente e parte literal por parte literal (por meio de propriedades de potência). Por exemplo:
4k(2x2 + 4xk + k2)
Multiplicando o monômio 4k por cada termo do polinômio, teremos:
4k·2x2 + 4k·4xk + 4k·k2
8k·x2 + 16xkk + 4k·k2
8k·x2 + 16xk2 + 4k3
Observe que as propriedades de potência foram usadas para unir as incógnitas idênticas em um fator único.
Quando os fatores da multiplicação são dois polinômios, é necessário multiplicar cada termo do primeiro por todos os termos do segundo. A propriedade que permite essa multiplicação é chamada de propriedade distributiva da multiplicação sobre a adição. Por exemplo:
(x – a)(x + a) =
xx + xa – xa – aa =
x2 + 0 – a2
x2 – a2
Por meio da multiplicação de polinômios, é possível definir produtos notáveis e prosseguir nos seus desdobramentos.
Divisão de polinômios
A divisão de polinômios segue as mesmas ideias usadas na divisão de números reais. Um dos polinômios é o divisor, outro é o dividendo, outro é o quociente, e o outro, o resto. Colocando divisor e dividendo em uma chave, podemos seguir o procedimento da divisão para buscar o resultado. Por exemplo:
10x2 – 43x + 40 |2x – 5
Na divisão numérica, devemos procurar um número que, multiplicado pelo divisor, aproxime-se ou seja igual ao dividendo. Na divisão de polinômios, procuramos por um monômio que, multiplicado pelo termo de grau mais alto do divisor, seja exatamente igual ao termo de grau mais alto do dividendo. No exemplo acima, procuramos por um monômio que, multiplicado por 2x, resulte em 10x2. Observe que 2·5 = 10 e x·x = x2. Assim, esse monômio é 5x.
Coloque esse monômio no quociente, multiplique-o pelo divisor e subtraia o resultado do dividendo.
10x2 – 43x + 40 |2x – 5
– (10x2 – 25x) 5x
Para agilizar os cálculos, dizemos que o resultado da multiplicação de 5x por 2x – 5 deve ser colocado com todos os sinais trocados sob o dividendo para que a subtração seja realizada:
10x2 – 43x + 40 |2x – 5
– 10x2 + 25x 5x
0 – 18x
Agora, basta “descer” o restante do dividendo e dar prosseguimento à divisão exatamente como feito no passo anterior.
10x2 – 43x + 40 |2x – 5
– 10x2 + 25x 5x – 9
0 – 18x + 40
18x – 45
– 5