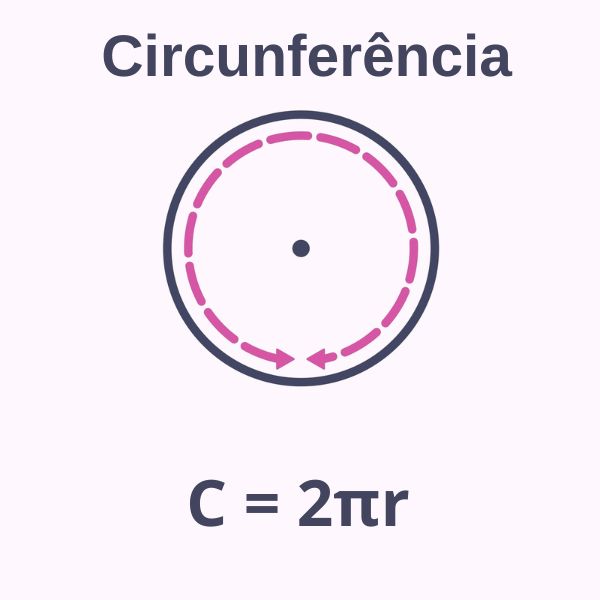
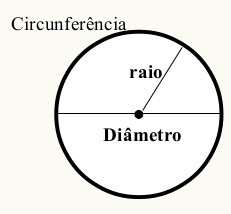
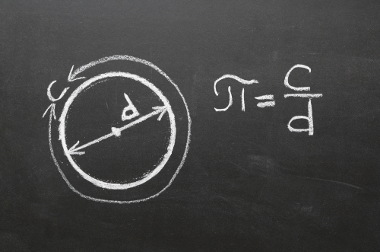Definimos circunferência como uma linha curva fechada que possui um ponto central, que, por sua vez, é chamado de origem (O) e é equidistante, ou seja, apresenta a mesma distância em todos os pontos da linha curva em relação ao centro. Toda circunferência possui raio e diâmetro. Veja:
Posições relativas entre as circunferências:
Existem seis posições relativas para as circunferências:
-
Posição 1: As circunferências não possuem ponto em comum externo.
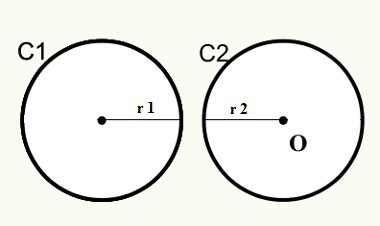
Observe que, na posição um, as circunferências C1 e C2 não se encontram, logo, não possuem ponto em comum externamente.
Representação da fórmula da distância
D > r1 + r2
D = Distância entre os centros/origens das circunferências
r1 = raio da circunferência C1
r2 = raio da circunferência C2
-
Posição 2: As circunferências não possuem ponto em comum interno.
.jpg)
Veja que as circunferências C1 e C2 não possuem um ponto em comum em relação às suas linhas curvas fechadas.
Representação da fórmula da distância
D < r1 – r2
D = Distância entre os centros/origens das circunferências
r1 = raio da circunferência C1
r2 = raio da circunferência C2
-
Posição 3: As circunferências possuem um ponto em comum externo. São chamadas de tangentes externas.
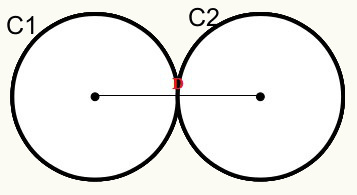
Temos que as circunferências C1 e C2 tocam-se em um ponto externo, logo, tangenciam-se externamente.
Representação da fórmula da distância
D = r1 + r2
D = Distância entre os centros/origens das circunferências.
r1 = raio da circunferência C1
r2 = raio da circunferência C2
-
Posição 4: As circunferências possuem um ponto em comum interno. São chamadas de tangentes internas.
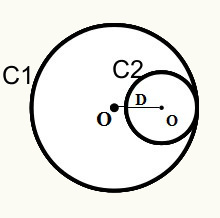
Representação da fórmula da distância
D = r1 – r2
D = Distância entre os centros/origens das circunferências.
r1 = raio da circunferência C1
r2 = raio da circunferência C2
As circunferências C1 e C2 tocam-se em um ponto. Quando isso acontece, dizemos que elas se tangenciam internamente.
-
Posição 5: As circunferências apresentam dois pontos em comum. Quando isso acontece, dizemos que elas são secantes.
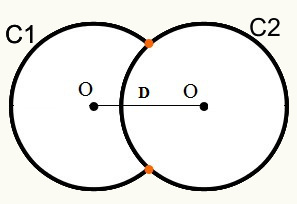
Veja que C1 e C2 interceptam-se em dois pontos, definidos na imagem pela cor laranja. Quando isso acontece, as circunferências são chamadas de secantes.
Representação da fórmula da distância
r1 – r2 < D < r1 + r2
D = Distância entre os centros/origens das circunferências.
r1 = raio de circunferência C 1
r2 = raio da circunferência C 2
-
Posição 6: Quando uma circunferência está dentro de outra, dizemos que elas são concêntricas. O centro/origem da circunferência é o mesmo. Com isso, não existe a necessidade de calcular a distância entre as origens, pois ela é zero.