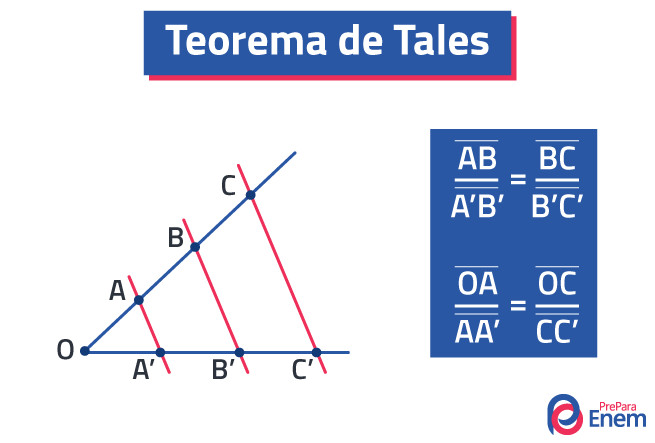
Reta é uma noção primitiva da Geometria, isto é, não existe definição para ela. Entretanto, é possível observar como as retas são formadas e os resultados de sua interação com outras figuras geométricas.
Uma reta é um conjunto de pontos que não faz curva, infinito e ilimitado. São as possíveis interações entre duas retas que constituem o estudo conhecido como posições relativas entre duas retas.
Se essas duas retas estão em um mesmo plano, existem três posições relativas que podem ser observadas: retas paralelas, concorrentes e coincidentes. Caso as retas não estejam no mesmo plano, é possível que elas sejam reversas ou caiam em algum dos casos já citados. Cada uma dessas definições será discutida a seguir.
Retas paralelas
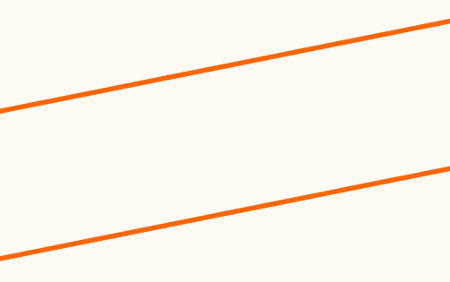
Quando duas retas pertencem a um mesmo plano, elas são chamadas de paralelas se não possuem nenhum ponto em comum. Não é possível que duas retas não pertencentes a um mesmo plano sejam paralelas, exceto quando for possível encontrar um plano que contenha as duas (mesmo que diferente dos planos iniciais).
Observe que a menor distância entre um ponto qualquer de uma das retas e a outra reta é sempre a mesma. Além disso, essas retas não possuem nenhum ponto em comum em toda a sua extensão, que é infinita.
Retas concorrentes
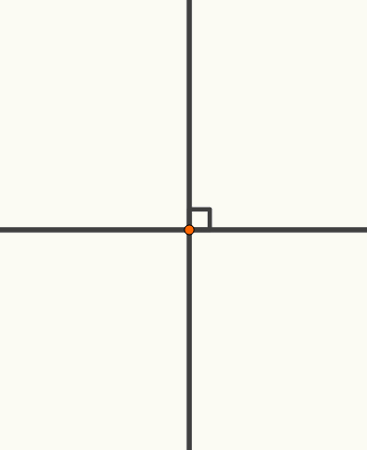
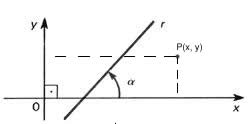
Duas retas são consideradas concorrentes quando existe apenas um ponto em comum entre elas. A imagem a seguir mostra um exemplo de duas retas concorrentes.
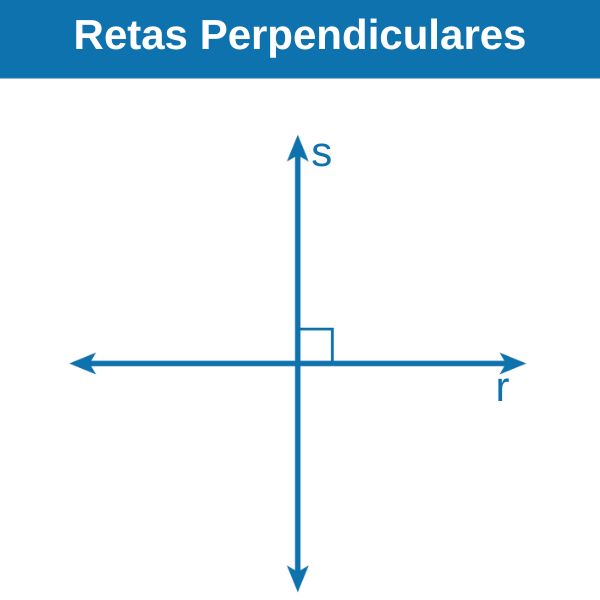
Quando o ângulo entre duas retas concorrentes é reto, dizemos que elas são perpendiculares, como mostra a figura acima.
Retas coincidentes
Quando duas retas possuem dois ou mais pontos em comum, existe uma propriedade que garante que elas apresentam todos os pontos em comum, ou seja, são coincidentes. Essas retas estão ocupando o mesmo espaço no plano, e pode-se também interpretá-las como se fossem uma reta só, como mostra o exemplo da imagem a seguir.
Retas reversas
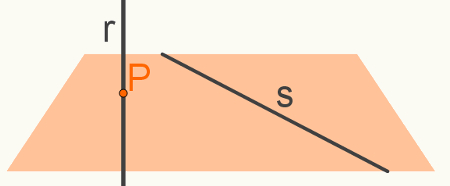
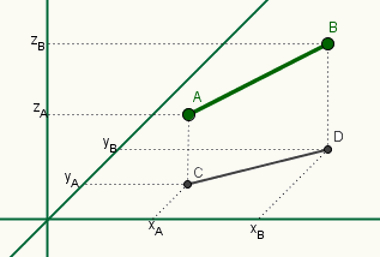
Retas reversas são aquelas que não pertencem a um mesmo plano. O exemplo a seguir mostra duas retas reversas. Observe que P é o ponto de encontro entre a reta r e o plano que contém a reta s. Como P não está sobre s, as retas não se encontram e nem podem pertencer a um mesmo plano.
Suponha que duas retas quaisquer sejam reversas. Se o ângulo entre essas duas retas é reto, então elas são ortogonais.
Videoaula relacionada: