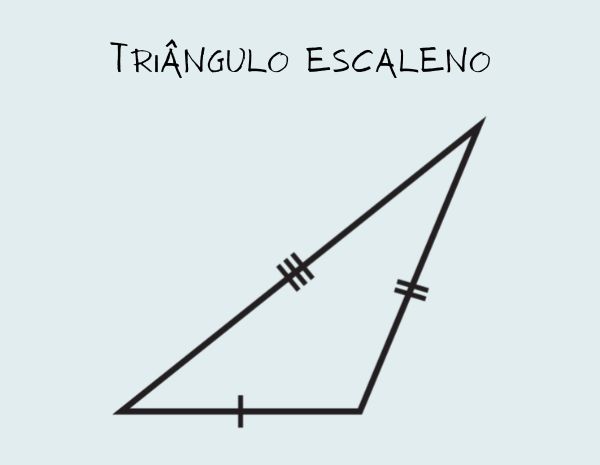
Triângulos são figuras matemáticas, pertencentes à área de estudo denominada geometria plana, que possuem três lados. Os lados são segmentos de reta, ou seja, um pedaço da reta: possuem um ponto inicial e um ponto final.
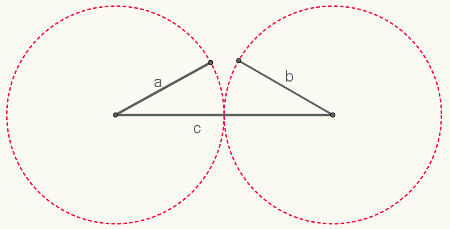
Os triângulos podem ser obtidos de diversas formas, a mais usual delas é desenhar 3 pontos não colineares (pontos que não pertencem a uma mesma reta) e ligá-los com segmentos de reta.
Alguns triângulos têm destaque na natureza e no dia a dia das pessoas por serem mais recorrentes, como é o caso dos triângulos retângulos que possuem um ângulo reto, isto é, um ângulo igual a 90 graus. Também ocorrem com frequência e possuem propriedades interessantes os triângulos isósceles e equiláteros. Esses nomes foram dados para classificá-los quanto aos seus lados, mas existe também uma classificação com relação aos ângulos de um triângulo.
Os triângulos isósceles são aqueles que possuem as medidas de pelo menos 2 de seus lados iguais. Já os triângulos equiláteros são aqueles que possuem as medidas de exatamente 3 de seus lados iguais.
Dito isso, observemos algumas propriedades envolvendo os triângulos isósceles e equiláteros:
Propriedade 1: Em um triângulo isósceles, as medidas dos ângulos da base são iguais.
Para observar que essa propriedade é válida, basta desenhar um triângulo isósceles, desenhar sua altura, mediana ou bissetriz e utilizar um dos casos de congruência de triângulos para verificá-la. Na figura a seguir, desenhamos a altura de um triângulo isósceles e destacamos as medidas que certamente são iguais.
.jpg)
Observe que “c” e “d” representam medidas dos lados desse triângulo e são iguais por que ele é isósceles. Os ângulos apontados com uma flecha também são iguais, ambos medem 90 graus, pois o segmento CD é altura. Observe também que o segmento CD é comum aos dois triângulos ACD e BCD. Essa configuração de lados e ângulos congruentes refere-se ao caso LAAo de congruência de triângulos. Sendo congruentes os dois triângulos, basta observar que os ângulos “a” e “b” são congruentes e a propriedade 1 fica demonstrada.
Propriedade 2: Em um triângulo isósceles, altura, mediana e bissetriz coincidem.
Aproveitando a imagem anterior AD = BD. Isso significa que a altura CD é também mediana. Além disso, como os triângulos são congruentes, então os ângulos “f” e “e” são iguais. Por isso, a altura CD é também bissetriz do triângulo ABC.
Quanto aos triângulos equiláteros
É importante lembrar que o triângulo equilátero recebe esse nome por que possui 3 lados iguais. Sendo assim, note que todo triângulo equilátero é também isósceles. Isso por que, olhando apenas dois de seus lados e ignorando o terceiro, observa-se um triângulo isósceles. Dessa forma, as duas propriedades acima são válidas para o triângulo equilátero assim como para o triângulo isósceles.
A novidade é que todos os ângulos de um triângulo equilátero são iguais e medem 60 graus. Os ângulos são iguais por que os lados são iguais. O valor deles é 60 graus por que a soma dos ângulos internos de um triângulo é 180 graus.