Problemas que podem ser resolvidos apenas com regra de três são muito frequentes em vestibulares e no Enem. Sendo assim, reunimos os três erros mais cometidos na hora de construir e resolver uma regra de três com o objetivo de ajudar os estudantes a não cometê-los mais.
Leia também: 3 macetes de Matemática para o Enem
1. Não interpretar corretamente o texto do problema
Esse é, sem dúvida, o erro mais frequente em todas as resoluções incorretas de exercícios. É muito comum que alunos encontrem (muitas vezes, de forma correta) o valor de x sem sequer ter lido o texto da questão, que, inclusive, não estava pedindo o valor de x. Para melhor ilustrar esse problema, observe o exemplo a seguir:
Na imagem abaixo, calcule a medida do segmento DF.
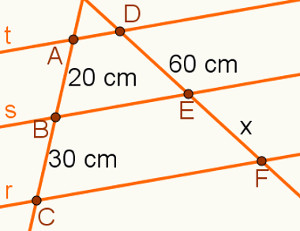
O primeiro passo é descobrir o valor de x por meio de uma regra de três:
20 = 60
30 x
20x = 30·60
x = 1800
20
x = 90
Observe que o valor de x não é o que o exercício pede. Sugerimos ao leitor que, ao terminar os cálculos, SEMPRE leia novamente o exercício, destacando o que ele pede como resultado final. Nesse caso, a questão solicita a soma das medidas dos segmentos DE com EF, que resulta na medida do segmento DF:
60 + 90 = 150 cm
2. Não observar se as grandezas são direta ou indiretamente proporcionais
Observe os dois exemplos a seguir para compreender o que são grandezas direta e inversamente proporcionais.
Exemplo 1:
Um automóvel desloca-se a 80 km/h e, durante determinado período de tempo, percorre 200 km. Qual seria o deslocamento desse automóvel se estivesse a 100 km/h?
Perceba que, com o aumento da velocidade, o espaço percorrido por um automóvel em um mesmo intervalo de tempo também aumenta. Da mesma forma, com a diminuição da velocidade, o espaço percorrido também diminui. Assim, dizemos que essas grandezas são diretamente proporcionais.
Podemos construir essa proporção da seguinte maneira:
80 = 200
100 x
80x = 100·200
x = 20000
80
x = 250 km
Exemplo 2:
Um automóvel desloca-se a 80 km/h e, a uma determinada velocidade média, demora 2 horas para alcançar seu destino. Quantas horas gastaria se sua velocidade média fosse 40 km/h?
Perceba que, com a diminuição da velocidade, o tempo gasto na viagem aumenta e, com o aumento da velocidade, o tempo de viagem diminui. Sendo assim, essas grandezas são inversamente proporcionais.
Assim, antes de aplicar a propriedade fundamental das proporções ou de pensar em resolver equações, devemos inverter uma das razões.
Veja a maneira correta de resolver uma regra de três de grandezas inversamente proporcionais:
80 = 2
40 x
80 = x
40 2
40x = 80·2
40x = 160
x = 160
40
x = 4 horas
Veja também: Quatro conteúdos básicos de Matemática para o Enem

3. Não seguir a ordem correta da proporção
Para toda proporção, existe uma ordem em que as medidas devem ser colocadas que deve ser seguida à risca. Para exemplificar essa ordem, observe o exemplo a seguir.
Exemplo:
Em uma fábrica de sapatos, 10 funcionários conseguem produzir 200 sapatos por dia. Quantos funcionários são necessários para produzir 250 sapatos?
As grandezas são diretamente proporcionais, por isso, na primeira fração, colocaremos a “situação inicial”, em que 10 funcionários produzem 200 sapatos, sendo 10 o numerador e 200 o denominador. A segunda “situação” é a que pergunta o número x de funcionários necessários para produzir 250 sapatos. Se o número de funcionários foi colocado no numerador da primeira fração, obrigatoriamente, terá que estar no numerador da segunda fração também.
10 = x
200 250
Há quem defenda até a construção de uma tabela para que não aconteçam erros nessa montagem.
Essa ordem é extremamente importante para a resolução correta da regra de três e é um dos erros mais cometidos pelos estudantes. O aluno simplesmente esquece que existe uma ordem e monta o exercício de qualquer maneira.
O restante da resolução do problema acima é o seguinte:
200x = 2500
x = 2500
200
x = 12,5
Como não é possível contratar meio funcionário, o número de funcionários necessários para produzir 250 sapatos é 13.