Chamamos de triângulo o polígono que possui três lados. Sendo o polígono com o menor número de lados, ele é o mais simples, porém com uma vasta aplicação no cotidiano. Os principais elementos de um triângulo são seus três lados e três ângulos.
Podemos classificar os triângulos analisando os seus lados (equilátero, isósceles e escaleno) ou de acordo com os seus ângulos (retângulo, acutângulo ou obtusângulo). Em um triângulo, a soma dos ângulos internos é sempre igual a 180°.
Para calcular o perímetro desse polígono, basta somar os seus lados. Já para obter o valor da área, calculamos o produto entre os comprimentos da base e da altura e dividimos o resultado por dois. Quando existem três segmentos, há uma condição para que eles formem um triângulo, conhecida como condição de existência de um triângulo.
Leia também: Quadrados — quadriláteros cujos lados e ângulos são congruentes
Tópicos deste artigo
- 1 - Resumo sobre triângulos
- 2 - Elementos de um triângulo
- 3 - Condição de existência de triângulos
- 4 - Propriedades do triângulo
- 5 - Classificação dos triângulos
- 6 - Perímetro de triângulo
- 7 - Altura do triângulo
- 8 - Área do triângulo
- 9 - Exercícios resolvidos sobre triângulos
Resumo sobre triângulos
-
O triângulo é um polígono.
-
O triângulo possui três lados e três ângulos.
-
A soma dos seus ângulos internos é igual a 180°.
-
Quando analisamos os ângulos de um triângulo, podemos classificá-los como:
-
Retângulo: possui um ângulo interno de 90°;
-
Acutângulo: possui os ângulos internos agudos;
-
Obtusângulo: possui um ângulo interno obtuso.
-
-
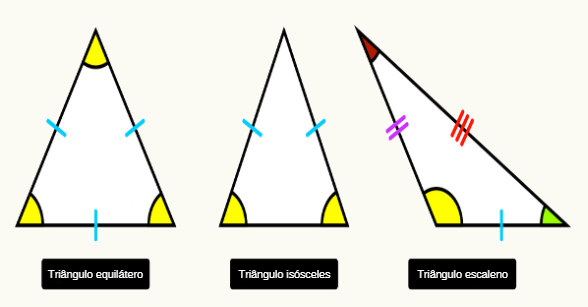
Quando analisamos os lados de triângulos, existem três classificações possíveis:
-
Equilátero: possui todos os lados congruentes;
-
Isósceles: possui dois lados congruentes;
-
Escaleno: possui todos os lados com medidas diferentes.
-
-
A condição de existência para um triângulo é que a soma do comprimento de dois lados é sempre maior que o terceiro lado.
-
Como nos demais polígonos, o perímetro de um triângulo é igual à soma dos seus três lados.
-
Para calcular a área do triângulo, utilizamos a fórmula:
![]()
Elementos de um triângulo
Para que uma figura geométrica seja conhecida como triângulo, é necessário que ela seja um polígono que possui exatamente três lados e três ângulos.
-
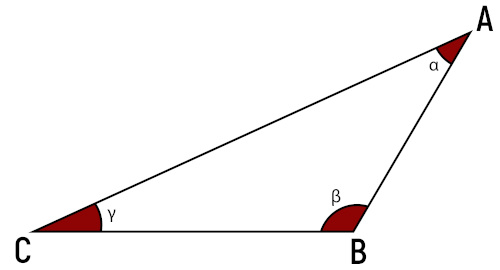
Os segmentos AB, AC e BC são os lados do triângulo;
-
Os pontos A, B e C são os vértices do triângulo;
-
Os ângulos α, β e ɣ são os ângulos internos do triângulo.
Condição de existência de triângulos
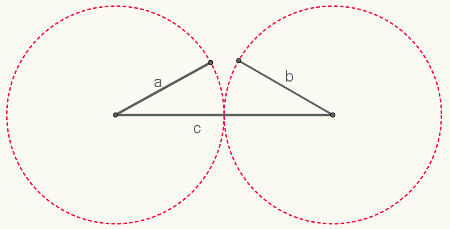
Três segmentos de reta podem ou não formar um triângulo. Para saber se é possível formar um triângulo conhecendo o comprimento desses três segmentos, é necessário verificar se a condição de existência do triângulo é atendida. Essa condição estabelece que a soma de dois lados é sempre menor que o terceiro lado.
Em um triângulo com lados medindo a, b e c, segundo a condição de existência, temos que:
a + b > c
b + c > a
a + c > b
Portanto, para verificar se é possível construir um triângulo conhecendo as medidas de seus segmentos, elas devem satisfazer a condição de existência.
-
Videoaula sobre condição de existência de triângulos
Propriedades do triângulo
Existem propriedades específicas para qualquer triângulo.
-
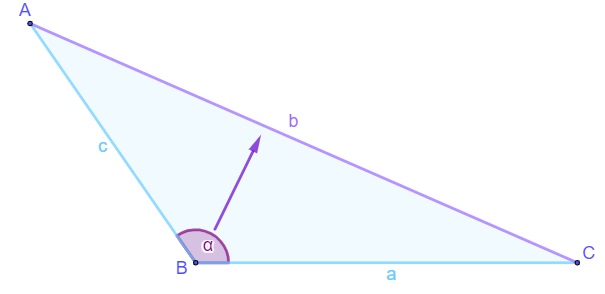
Dado um triângulo de ângulos internos α, β e ɣ, a soma desses ângulos é sempre igual a 180°, ou seja:
α + β + ɣ = 180°
-
Em um triângulo, o maior lado fica sempre oposto ao maior ângulo e o menor lado fica sempre oposto ao menor ângulo.
Classificação dos triângulos
Existem duas maneiras distintas de se classificar os triângulos. Uma delas é a classificação quanto aos ângulos e a outra é quanto a seus lados.
-
Classificação dos triângulos quanto aos ângulos
Quando analisamos seus ângulos, pode-se classificar um triângulo em três tipos diferentes:
-
triângulo acutângulo;
-
triângulo retângulo;
-
triângulo obtusângulo.
-
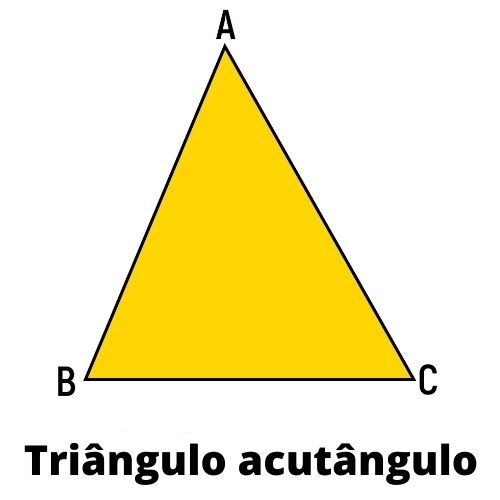
Triângulo acutângulo
-
Um triângulo é acutângulo quando todos os seus ângulos internos são agudos, ou seja, menores que 90°.
-
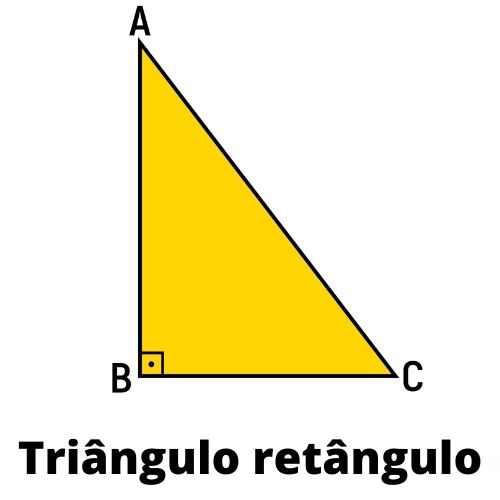
Triângulo retângulo
Um triângulo é retângulo quando ele possui um ângulo interno reto, ou seja, igual a 90°.
-
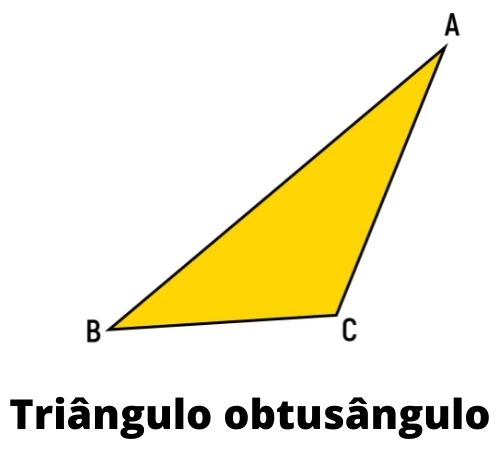
Triângulo obtusângulo
Um triângulo é obtusângulo quando ele possui um ângulo interno obtuso, ou seja, maior que 90°.
-
Classificação dos triângulos quanto aos lados
Outra maneira de classificar os triângulos é fazendo a comparação entre as medidas dos seus lados. Nesse caso, também há três tipos de triângulos, sendo eles:
-
triângulo equilátero;
-
triângulo isósceles;
-
triângulo escaleno.
-
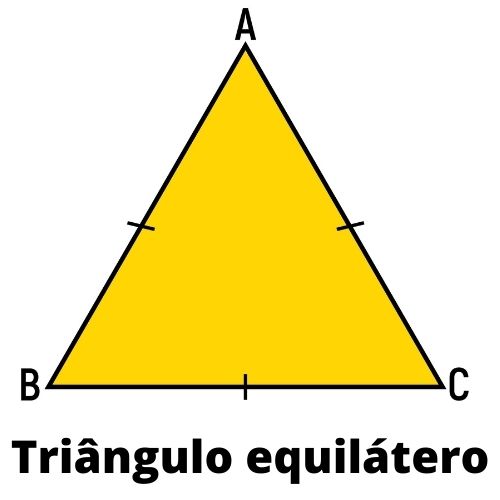
Triângulo equilátero
-
Um triângulo é equilátero quando ele possui os três lados congruentes, ou seja, todos os lados possuem a mesma medida.
-
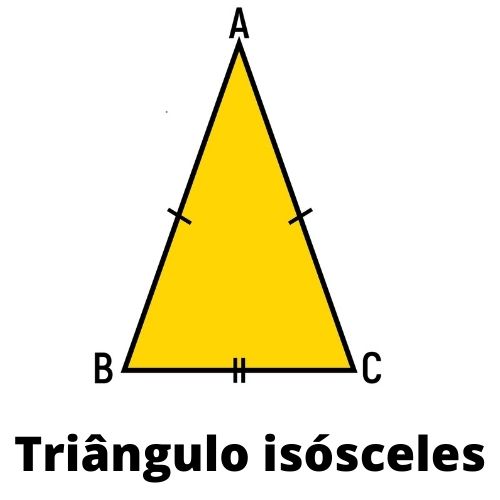
Triângulo isósceles
Um triângulo é isósceles quando ele possui dois lados congruentes.
-
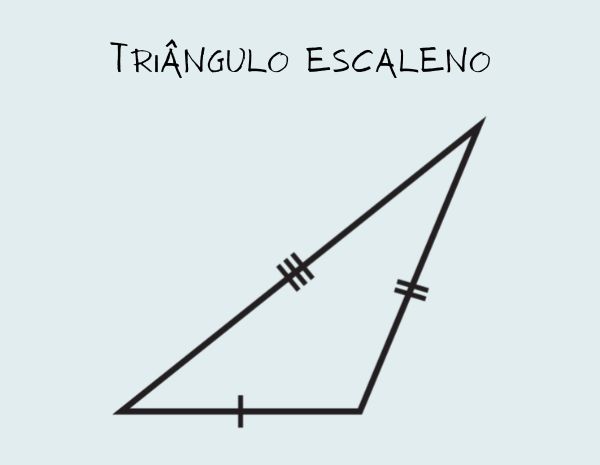
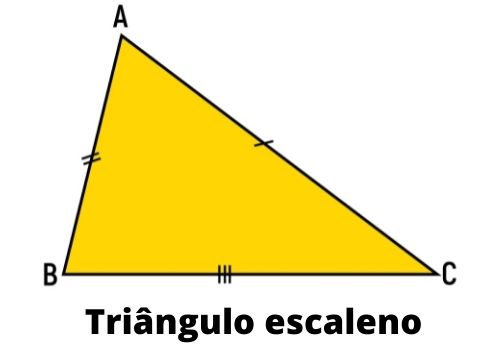
Triângulo escaleno
Um triângulo é escaleno quando ele possui todos os lados com medidas distintas.
Perímetro de triângulo
O perímetro é o comprimento do contorno de um polígono. Para saber o comprimento total do contorno de qualquer polígono, incluindo o triângulo, basta realizar a soma de todos os seus lados.
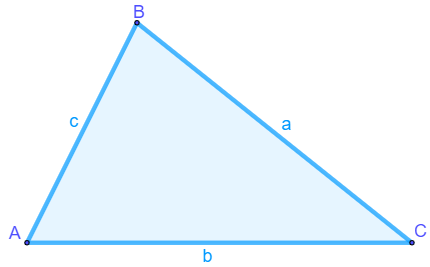
|
P = a + b + c |
Exemplo:
Dado o triângulo a seguir, calcule o seu perímetro:
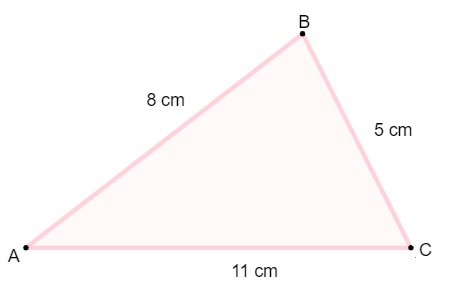
Resolução:
P = 8 + 5 + 11 = 24 cm
Leia também: Propriedades do triângulo isósceles e do equilátero
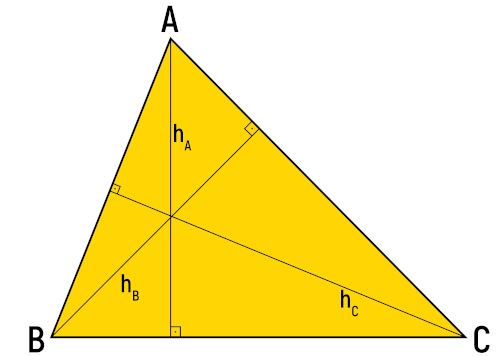
Altura do triângulo
A altura é o segmento entre o vértice oposto a um lado e esse lado, formando um ângulo de 90° com a base do triângulo. Como qualquer um dos três lados do triângulo pode ser tratado como base, é possível traçar três alturas no triângulo, cada uma partindo de um vértice.
Área do triângulo
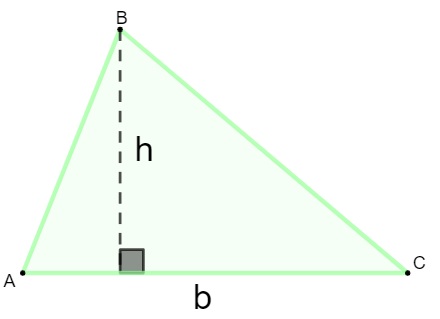
Para calcular a área de um triângulo, é necessário conhecer o comprimento da sua base e da altura relativa a essa base. Sendo b o comprimento da base e h o comprimento da altura, a área do triângulo é calculada por:
![]()
Exemplo:
Encontre a área de um triângulo que possui base medindo 18 cm e altura igual a 12 cm.
Resolução:
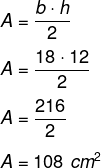
Leia também: Casos de congruência de triângulos
Exercícios resolvidos sobre triângulos
Questão 1
Ao fazer pesquisas sobre desmatamento, o Inpe constatou que uma área de 10.476 km² foi desmatada. Para fazer a representação dessa área geometricamente, o melhor polígono a ser escolhido foi um triângulo, que possui base igual a 216 km. Portanto, a altura desse triângulo deve ser de:
A) 85 km.
B) 97 km.
C) 100 km.
D) 112 km.
E) 125 km.
Resolução:
Alternativa B
Considerando a área do terreno, temos que:
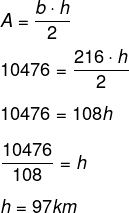
Questão 2
Sobre o triângulo, julgue as afirmativas a seguir:
I → Todo triângulo retângulo é escaleno.
II → Todo triângulo equilátero é acutângulo.
III → Um triângulo isósceles pode ser obtusângulo.
Estão corretas:
A) Somente a afirmativa I.
B) Somente a afirmativa II.
C) Somente a afirmativa III.
D) Somente as afirmativas I e II.
E) Somente as afirmativas II e III.
Resolução:
Alternativa E
I → (Falsa)
O triângulo retângulo pode ser escaleno ou isósceles. Logo, nem todo triângulo retângulo é escaleno.
II → (Verdadeira)
O triângulo equilátero possui ângulos internos congruentes (180 : 3 = 60°). Como cada um deles mede 60°, todos os ângulos são agudos. Assim, o triângulo equilátero será sempre acutângulo.
III → (Verdadeira)
O triângulo isósceles possui dois lados congruentes. Dessa forma, dois de seus ângulos são congruentes também, o que torna possível que exista um triângulo isósceles que seja obtusângulo.