Conforme nos mostra o texto “Transformações gasosas”, os estudos de três cientistas foram imprescindíveis para o entendimento do comportamento dos gases em relação às suas variáveis de estado, que são o volume, a pressão e a temperatura. Os cientistas em questão são: Robert Boyle (1627-1691) e os cientistas franceses Joseph Louis Gay-Lussac (1778-1850) e Jacques Alexandre César Charles (1746-1823).
Abaixo temos um quadro com um resumo das conclusões tiradas por cada um desses cientistas e as fórmulas matemáticas que exprimem isso:

Observe que em todas as transformações o valor representado é o k. Assim, podemos realizá-las simultaneamente e, desse modo, relacionar as três variáveis de estado em uma única equação. Observe abaixo como ocorre a junção dessas três equações:

Assim, a equação geral dos gases ou equação da transformação geral dos gases é dada por: .jpg)
Isso quer dizer que quando uma massa fixa de gás sofre uma transformação em que as três grandezas (pressão, temperatura e volume) se alteram, a relação PV/T permanece constante.
Essa equação é bastante útil para se determinar o novo estado do gás que sofreu alteração. Por exemplo, se conhecermos o volume de um gás x em determinadas condições de temperatura e pressão, utilizando essa equação podemos determinar seu novo volume em outras condições de temperatura e pressão. O mesmo pode ser feito no caso da temperatura e da pressão.
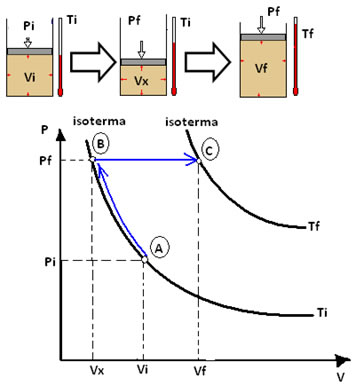
O gráfico da transformação de estado que ocorre ao mesmo tempo com as três variáveis resulta em hipérboles isotermas. Veja o exemplo abaixo:
Determinado gás teve sua pressão e volume variados, sendo que a temperatura permaneceu constante, assim, temos que Vi passou para Vx e Pi para Px, que é o mesmo que Pf, pois não mudou-se mais a pressão. Dessa forma, obtemos a seguinte equação:
Pi . Vi = Pf . Vx
Posteriormente, manteve-se a pressão constante e variou-se o volume e a temperatura. Vx variou para Vf e Ti para Tf. Uma segunda equação foi obtida:
Vx = Vf
Ti Tf
Multiplicando as duas equações obtidas, temos:
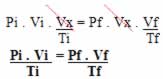
Chegamos exatamente na equação geral dos gases, que pode ser representada graficamente pelas duas isotermas a seguir: